Introduction
In this example, we check the correctness of SFEMaNS for a magnetohydrodynamic problem. This test uses Dirichlet, Neumann and periodic boundary conditions. We note this test does not involve manufactured solutions and consist of checking four quantities, like the \(\bL^2\) norm of the velocity, are the same than the values of reference.
We solve the Navier-Stokes equations:
\begin{align*} \partial_t\bu+\left(\ROT\bu + 2 \epsilon \textbf{e}_z \right)\CROSS\bu - \frac{1}{\Re}\LAP \bu +\GRAD p &= (\ROT \textbf{H}) \times (\mu^c \textbf{H}), \\ \DIV \bu &= 0, \\ \bu_{|\{z=0\}} &= \bu_{|\{z=1\}} , \\ \bu_{|\Gamma} &= \bu_{\text{bdy}} , \\ \bu_{|t=0} &= \bu_0, \\ p_{|t=0} &= p_0, \end{align*}
and the Maxwell equations:
\begin{align*} \partial_t (\mu^c \mathbf{H}) + \nabla \times \left(\frac{1}{\Rm \sigma}\nabla \times \mathbf{H} \right) & = \nabla\times (\bu \times \mu^c \mathbf{H}), \\ \text{div} (\mu^c \mathbf {H}) &= 0 ,\\ \mathbf{H}_{|\{z=0\}} &= \mathbf{H}_{|\{z=1\}} , \\ \left( \frac{1}{\Rm \sigma} \left( \ROT (\mathbf{H}) - \mathbf{j} \right) - \bu \times \mu \mathbf{H} \right) \times \bn_{|\Gamma} & = {\textbf{a} \times \bn}_{|\Gamma},\\ \bH_{|t=0}&= \bH_0. \end{align*}
Theses equations are solved in the domain \(\Omega= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in [0,1/2] \times [0,2\pi) \times [0,1]\} \) with \(\Gamma= \partial \Omega\setminus\{ \{z=0\} \cup \{z=1\} \} \). The data are the boundary datas \(\bu_{\text{bdy}}, \textbf{a}\), the initial data \(\bu_0, p_0, \bH_0\). The parameters are the kinetic Reynolds number \(\Re\), the magnetic Reynolds number \(\Rm\), the magnetic permeability \(\mu^c\) and the conductivity \(\sigma\) of the fluid.
Manufactured solutions
As mentionned earlier this test does not involve manufactured solutions. As a consequence, we do not consider specific source term and only initialize the variables to approximate.
The initial velocity field and pressure are set to zero.
\begin{align*} u_r(r,\theta,z,t=0) &= 0.5 - r, \\ u_{\theta}(r,\theta,z,t=0) &= (r-0.5)r\sin(2\pi z), \\ u_z(r,\theta,z,t=0) &= 0, \\ p(r,\theta,z,t=0) &= 0. \end{align*}
The magnetic field is iniatialized as follows:
\begin{align*} \\ H_r(r,\theta,z,t=0) &= 0, \\ H_{\theta}(r,\theta,z,t=0) &= r, \\ H_z(r,\theta,z,t=0) &= 1 + r(r-0.5)\left(\cos(\theta)+\sin(\theta)+ \cos(2\theta)+\sin(2\theta)\right). \end{align*}
The boundary datas \(\bu_{\text{bdy}}, \textbf{a}\) are set to zero.
Generation of the mesh
The finite element mesh used for this test is named Mesh_20_form.FEM. The mesh size is \(0.05\) for the P1 approximation. You can generate this mesh with the files in the following directory: ($SFEMaNS_MESH_GEN_DIR)/EXAMPLES/EXAMPLES_MANUFACTURED_SOLUTIONS/Mesh_20_form. The following image shows the mesh for P1 finite elements.
Finite element mesh (P1).
|
Information on the file condlim.f90
The initial conditions, boundary conditions and the forcing terms are set in the file condlim_test_13.f90. Here is a description of the subroutines and functions of interest.
-
The subroutine
init_velocity_pressure initializes the velocity field and the pressure at the time \(-dt\) and \(0\) with \(dt\) being the time step. It is done by using the functions vv_exact and pp_exact as follows: time = 0.d0
DO i= 1, SIZE(list_mode)
mode = list_mode(i)
DO j = 1, 6
!===velocity
un_m1(:,j,i) = vv_exact(j,mesh_f%rr,mode,time-dt)
un (:,j,i) = vv_exact(j,mesh_f%rr,mode,time)
END DO
DO j = 1, 2
!===pressure
pn_m2(:) = pp_exact(j,mesh_c%rr,mode,time-2*dt)
pn_m1 (:,j,i) = pp_exact(j,mesh_c%rr,mode,time-dt)
pn (:,j,i) = pp_exact(j,mesh_c%rr,mode,time)
phin_m1(:,j,i) = pn_m1(:,j,i) - pn_m2(:)
phin (:,j,i) = Pn (:,j,i) - pn_m1(:,j,i)
ENDDO
ENDDO
-
The function
vv_exact contains the analytical velocity field. It is used to initialize the velocity field and to impose Dirichlet boundary conditions on the velocity field.
-
We construct the radial and vertical coordinates r, z.
-
For a time stritly larger than 0, we set the Dirichlet boundary condition to zero.
-
For the initialization, if the Fourier mode m is not equal to 0, the velocity field is set to zero.
ELSE
IF (m/=0) THEN
vv = 0.d0
-
For the Fourier mode \(m=0\), we define the velocity field depending of its TYPE (1 and 2 for the component radial cosine and sine, 3 and 4 for the component azimuthal cosine and sine, 5 and 6 for the component vertical cosine and sine) as follows:
ELSE
IF (TYPE==1) THEN
vv = 0.5-r
ELSE IF (TYPE==3) THEN
vv = (r-0.5)*r*SIN(2*PI*
z)
ELSE
vv = 0.d0
END IF
END IF
END IF
RETURN
-
The function
pp_exact contains the analytical pressure. It is used to initialize the pressure and is set to zero.
-
The function
source_in_NS_momentum is used to define the source term \(\bef\) of the Navier-Stokes equations. As this term is not used for this test, it is set to zero.
-
The subroutine
init_maxwell initializes the magnetic field at the time \(-dt\) and \(0\) with \(dt\) being the time step. It is done by using the functions Hexact as follows: time = -dt
DO k=1,6
DO i=1, SIZE(list_mode)
Hn1(:,k,i) = Hexact(H_mesh,k, H_mesh%rr, list_mode(i), mu_H_field, time)
IF (inputs%nb_dom_phi>0) THEN
IF (k<3) THEN
phin1(:,k,i) = Phiexact(k, phi_mesh%rr, list_mode(i) , mu_phi, time)
ENDIF
END IF
ENDDO
ENDDO
time = time + dt
DO k=1,6
DO i=1, SIZE(list_mode)
Hn(:,k,i) = Hexact(H_mesh,k, H_mesh%rr, list_mode(i), mu_H_field, time)
IF (inputs%nb_dom_phi>0) THEN
IF (k<3) THEN
phin(:,k,i) = Phiexact(k, phi_mesh%rr, list_mode(i), mu_phi, time)
ENDIF
END IF
ENDDO
-
The function
Hexact contains the analytical magnetic field. It is used to initialize the magnetic field.
-
For the Fourier mode \(m\in\{1,2\}\), we define the magnetic field depending of its TYPE (1 and 2 for the component radial cosine and sine, 3 and 4 for the component azimuthal cosine and sine, 5 and 6 for the component vertical cosine and sine) as follows:
IF (m/=0) THEN
IF (TYPE==5 .OR. TYPE==6) THEN
vv = rr(1,:)*(rr(1,:)-0.5)
ELSE
vv = 0.d0
END IF
-
For the Fourier mode \(m=0\), we define the magnetic field depending of its TYPE (1 and 2 for the component radial cosine and sine, 3 and 4 for the component azimuthal cosine and sine, 5 and 6 for the component vertical cosine and sine) as follows:
ELSE
IF (TYPE==3) THEN
vv = rr(1,:)
ELSE IF (TYPE==5) THEN
vv = 1.d0
ELSE
vv = 0.d0
END IF
END IF
RETURN
-
The function
Jexact_gauss is used to define the source term \(\textbf{j}\) that is not used in this test. So we set it to zero.
-
The function
Eexact_gauss is used to define the boundary data \(\textbf{a}\). It is set to zero.
All the other subroutines present in the file condlim_test_13.f90 are not used in this test. We refer to the section Fortran file condlim.f90 for a description of all the subroutines of the condlim file.
Setting in the data file
We describe the data file of this test. It is called debug_data_test_13 and can be found in the following directory: ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
-
We use a formatted mesh by setting:
===Is mesh file formatted (true/false)?
.t.
-
The path and the name of the mesh are specified with the two following lines:
===Directory and name of mesh file
'.' 'Mesh_20_form.FEM'
-
We use one processor in the meridian section. It means the finite element mesh is not subdivised. To do so, we write:
===Number of processors in meridian section
1
-
We solve the problem for \(3\) Fourier modes.
===Number of Fourier modes
3
-
We use \(3\) processors in Fourier.
===Number of processors in Fourier space
3
-
We select specific Fourier modes to solve.
===Select Fourier modes? (true/false)
-
We give the list of the Fourier modes to solve.
===List of Fourier modes (if select_mode=.TRUE.)
0 1 2
-
We approximate the Maxwell and the Navier-Stokes equations by setting:
===Problem type: (nst, mxw, mhd, fhd)
'mhd'
-
We do not restart the computations from previous results.
===Restart on velocity (true/false)
.f.
===Restart on magnetic field (true/false)
.f.
-
We use a time step of \(0.02\) and solve the problem over \(10\) time iterations.
===Time step and number of time iterations
2d-2, 20
-
We set periodic boundary condition.
-
We set the number of pair of boundaries that has to be periodic.
-
We give the label of the boundaries and the vector that lead to the first boundary to the second one.
===Indices of
periodic boundaries and corresponding vectors
4 2 .0d0 1.d0
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the Navier-Stokes equations,
===Number of subdomains in Navier-Stokes mesh
1
===List of subdomains for Navier-Stokes mesh
1
-
We set the number of boundaries with Dirichlet conditions on the velocity field and give their respective labels.
===How many
boundary pieces
for full Dirichlet BCs on velocity?
1
===List of
boundary pieces
for full Dirichlet BCs on velocity
5
-
We set the kinetic Reynolds number \(\Re\).
-
We give information on how to solve the matrix associated to the time marching of the velocity.
-
===Maximum number of iterations for velocity solver
100
-
===Relative tolerance for velocity solver
1.d-6
===Absolute tolerance for velocity solver
1.d-10
-
===Solver type for velocity (FGMRES, CG, ...)
GMRES
===Preconditionner type for velocity solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
We give information on how to solve the matrix associated to the time marching of the pressure.
-
===Maximum number of iterations for pressure solver
100
-
===Relative tolerance for pressure solver
1.d-6
===Absolute tolerance for pressure solver
1.d-10
-
===Solver type for pressure (FGMRES, CG, ...)
GMRES
===Preconditionner type for pressure solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
We give information on how to solve the mass matrix.
-
===Maximum number of iterations for mass matrix solver
100
-
===Relative tolerance for mass matrix solver
1.d-6
===Absolute tolerance for mass matrix solver
1.d-10
-
===Solver type for mass matrix (FGMRES, CG, ...)
CG
===Preconditionner type for mass matrix solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the magnetic field.
===Number of subdomains in magnetic field (H) mesh
1
===List of subdomains for magnetic field (H) mesh
1
-
We set the number of interface in H_mesh.
===Number of interfaces in H mesh
0
-
We set the number of boundaries with Dirichlet conditions on the magnetic field and give their respective labels.
===Number of Dirichlet sides for Hxn
0
===List of Dirichlet sides for Hxn
0
-
We set the magnetic permeability in each domains where the magnetic field is approximated.
===Permeability in the conductive part (1:nb_dom_H)
1.d0
-
We set the conductivity in each domains where the magnetic field is approximated.
===Conductivity in the conductive part (1:nb_dom_H)
1.d0
-
We set the type of finite element used to approximate the magnetic field.
===Type of finite element for magnetic field
2
-
We set the magnetic Reynolds number \(\Rm\).
===Magnetic Reynolds number
1.d0
-
We set stabilization coefficient for the divergence of the magnetic field and the penalty of the Dirichlet and interface terms.
===Stabilization coefficient (divergence)
1.d0
===Stabilization coefficient for Dirichlet H and/or interface H/H
1.d0
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the scalar potential.
===Number of subdomains in magnetic potential (phi) mesh
0
-
We give information on how to solve the matrix associated to the time marching of the Maxwell equations.
-
===Maximum number of iterations for Maxwell solver
100
-
===Relative tolerance for Maxwell solver
1.d-6
===Absolute tolerance for Maxwell solver
1.d-10
-
===Solver type for Maxwell (FGMRES, CG, ...)
GMRES
===Preconditionner type for Maxwell solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
To get the total elapse time and the average time in loop minus initialization, we write:
===Verbose timing? (true/false)
lis when you run the shell debug_SFEMaNS_template.
Outputs and value of reference
The outputs of this test are computed with the file post_processing_debug.f90 that can be found in the following directory: ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
To check the well behavior of the code, we compute four quantities:
-
The H1 norm of the velocity.
-
The L2 norm of the magnetic field divergence.
-
The L2 norm of the magnetic field.
-
The L2 norm of the pressure.
These quantities are computed at the final time \(t=0.2\). They are compared to reference values to attest of the correctness of the code. These values of reference are in the last lines of the file debug_data_test_13 in the directory ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC. They are equal to:
============================================
Mesh_20_form.FEM, P2
===Reference results
3.506833380349648E-002 H1 norm on velocity
3.720369285322975E-006 L2 norm of div(Hn)
0.886235556266004 L2 norm of Hn
2.313775787175324E-003 L2 norm of pressure
To conclude this test, we show the profile of the approximated pressure, velocity magnitude and magnetic field magnitude at the final time. These figures are done in the plane \(y=0\) which is the union of the half plane \(\theta=0\) and \(\theta=\pi\).
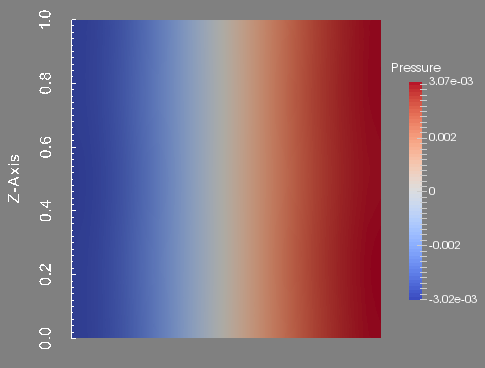
Pressure in the plane plane y=0.
|
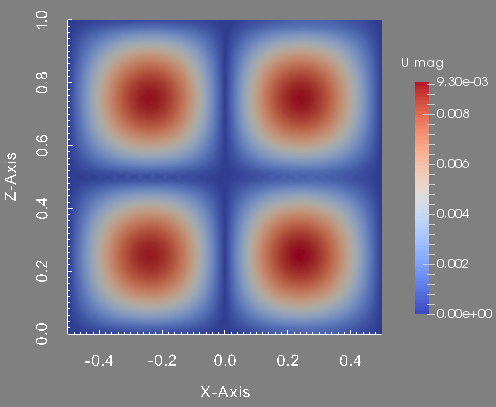
Velocity magnitude in the plane plane y=0.
|
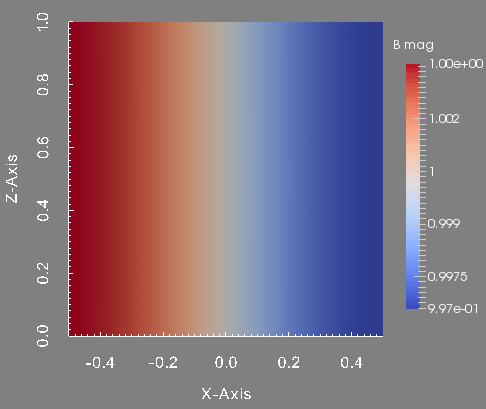
Magnetic field magnitude in the plane plane y=0.
|





