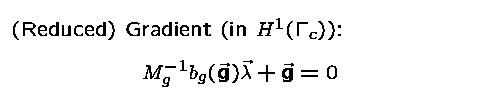The First Order Optimality Conditions
for the Discretized Problem
If we consider the discretized optimization
problem as a finite dimensional in
 then the following optimality conditions
arise
(subscripts denote partial derivatives):
then the following optimality conditions
arise
(subscripts denote partial derivatives):
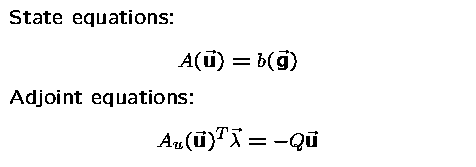
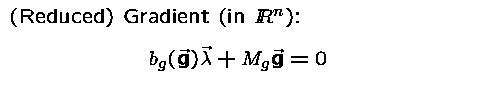
If one compares these optimality conditions
with the
optimiality conditions for the
infinite dimensional problem ,
then one observes in a difference in the
formula for the gradient.
This difference is due to the fact that here
we have neglected the infinite dimensional
structure and computed the gradient with respect
to the Euclidean scalar product in 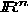 .
.
If we use the scalar product 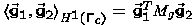 for the controls, which is the proper discretization of
the scalar product in
for the controls, which is the proper discretization of
the scalar product in 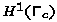 ,
then the gradient equation is given by
,
then the gradient equation is given by
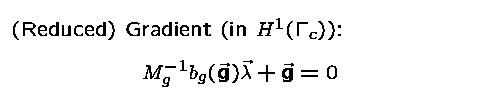
This formulation of the reduced gradient
and the use of the weighted scalar product
corresponds to the infinite dimensional
formulation. We will see that this is crucial
to compute meaningful controls.
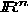 then the following optimality conditions
arise
(subscripts denote partial derivatives):
then the following optimality conditions
arise
(subscripts denote partial derivatives): 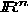 then the following optimality conditions
arise
(subscripts denote partial derivatives):
then the following optimality conditions
arise
(subscripts denote partial derivatives): 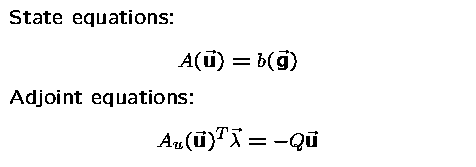
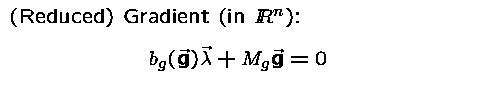
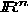 .
.
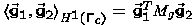 for the controls, which is the proper discretization of
the scalar product in
for the controls, which is the proper discretization of
the scalar product in 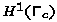 ,
then the gradient equation is given by
,
then the gradient equation is given by