Using the two photointerruptors described above, we record string displacement
data in two axes. Each of the plots that follow below show data for both
axes: one plotted in blue, the other in green.
(In some cases, the green data obscures the blue.)
|
Two bead data |
|
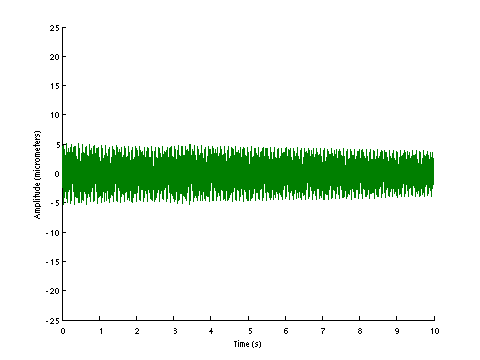
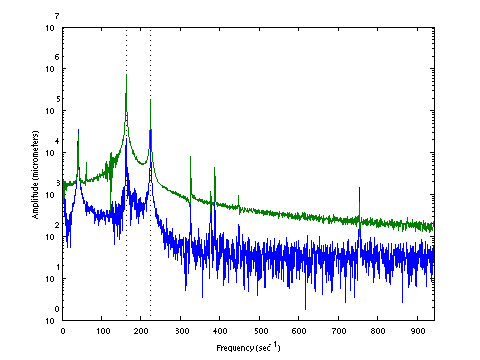
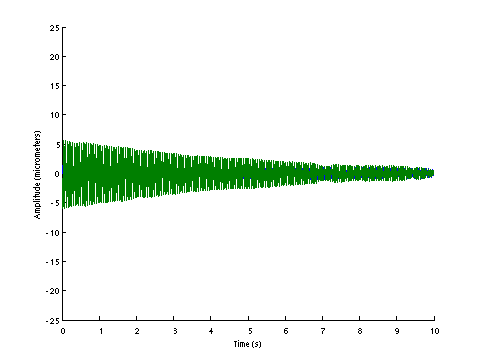
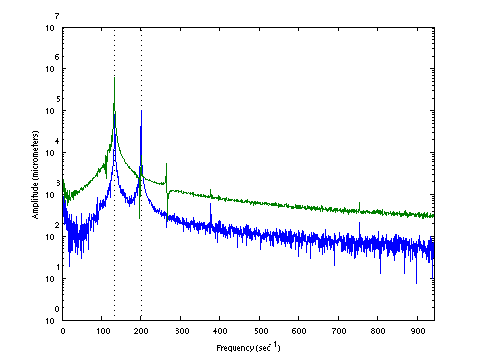
| D0132 dataset solution |
 |
| ω | = | 162.73, | 224.31 | sec-1 |
| Λ | = | 26483, | 50315 |
σ = 125.3 N , L = 1.124 m
|
 |  |
|
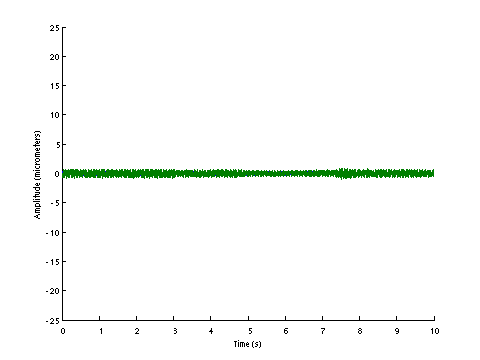
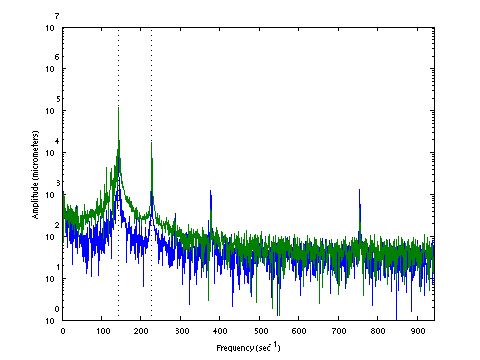
| D0134 dataset solution |
 |
| ω | = | 143.26, | 227.45 | sec-1 |
| Λ | = | 20522, | 51734 |
σ = 126.1 N , L = 1.124 m
|
 |  |
|
| D0166 dataset solution |
 |
| ω | = | 133.20, | 200.43 | sec-1 |
| Λ | = | 17743, | 40174 |
σ = 163.1 N , L = 1.124 m
|
 |  |
|
Four bead data |
|
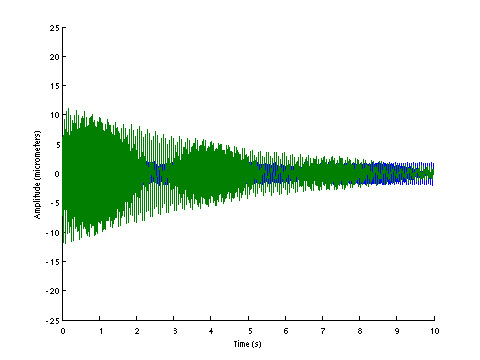
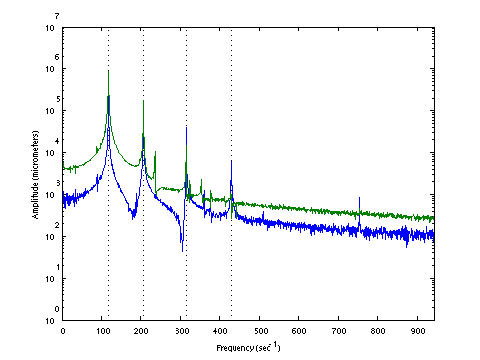
| D0139 dataset solution |
 |
| ω | = | 118.12, | 206.72, | 315.42, | 429.14 | sec-1 |
| Λ | = | 13953, | 42732, | 99487, | 184162 |
σ = 191.8 N , L = 1.124 m
|
 |  |
|
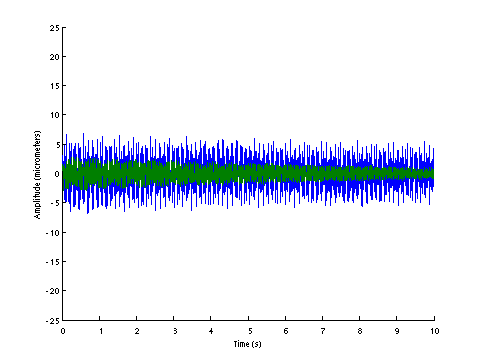
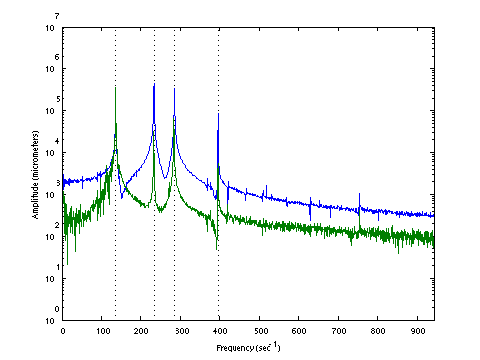
| D0142 dataset solution |
 |
| ω | = | 135.72, | 233.11, | 284.63, | 395.84 | sec-1 |
| Λ | = | 18419, | 54338, | 81013, | 156690 |
σ = 191.2 N , L = 1.124 m
|
 |  |
|
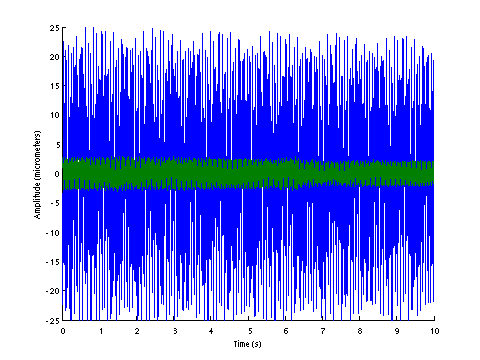
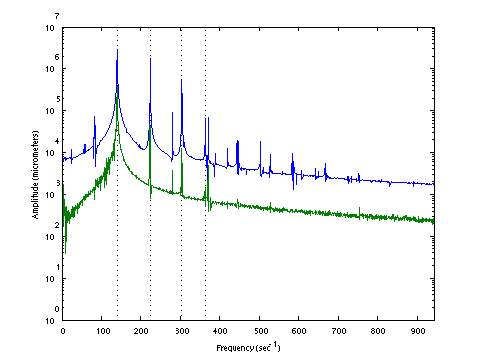
| D0144 dataset solution |
 |
| ω | = | 139.49, | 223.68, | 303.48, | 363.17 | sec-1 |
| Λ | = | 19457, | 50033, | 92099, | 131891 |
σ = 192.5 N , L = 1.124 m
|
 |  |
|
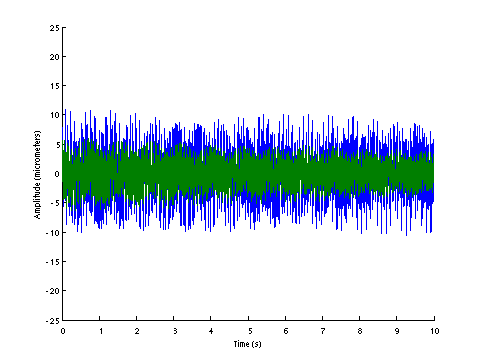
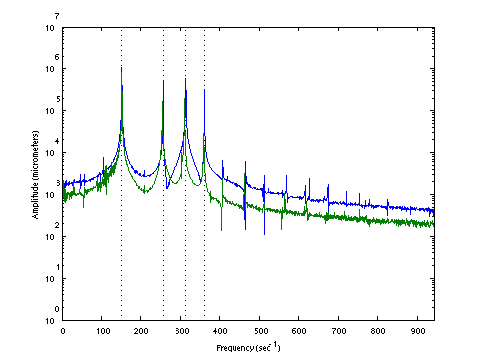
| D0146 dataset solution |
 |
| ω | = | 151.42, | 256.35, | 313.53, | 360.65 | sec-1 |
| Λ | = | 22929, | 65717, | 98302, | 130072 |
σ = 192.5 N , L = 1.124 m
|
 |  |
|
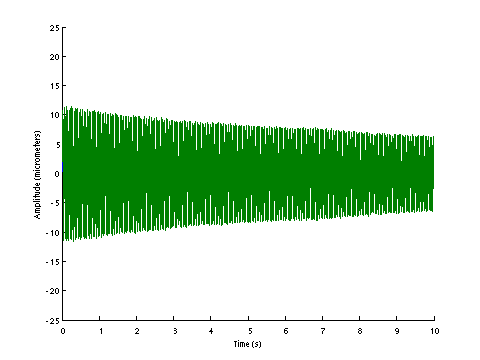
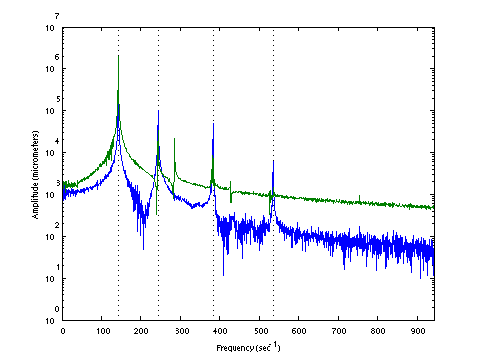
| D0148 dataset solution |
 |
| ω | = | 142.63, | 244.42, | 382.65, | 534.70 | sec-1 |
| Λ | = | 20343, | 59739, | 146418, | 285903 |
σ = 154.2 N , L = 1.124 m
|
 |  |
|
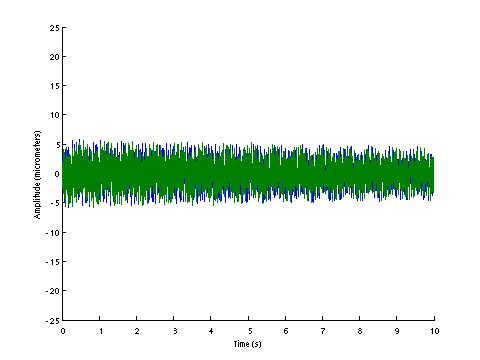
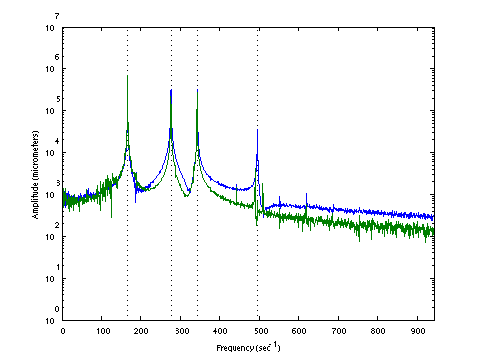
| D0149 dataset solution |
 |
| ω | = | 166.50, | 276.46, | 343.06, | 495.12 | sec-1 |
| Λ | = | 27724, | 76430, | 117691, | 245139 |
σ = 154.0 N , L = 1.124 m
|
 |  |
|
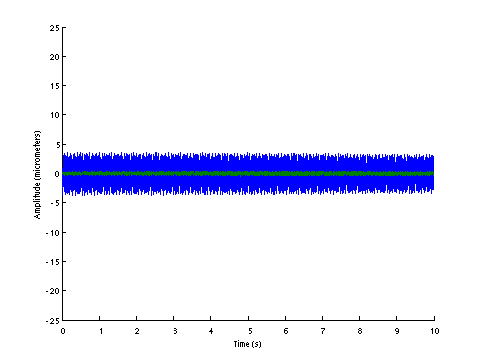
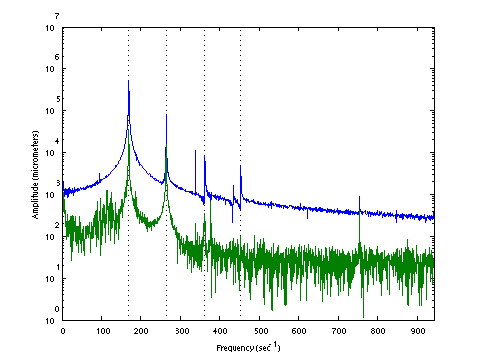
| D0151 dataset solution |
 |
| ω | = | 169.65, | 264.52, | 361.91, | 453.02 | sec-1 |
| Λ | = | 28780, | 69972, | 130980, | 205225 |
σ = 152.9 N , L = 1.124 m
|
 |  |
|
| D0152 dataset solution |
 |
| ω | = | 164.62, | 273.32, | 339.92, | 490.09 | sec-1 |
| Λ | = | 27100, | 74703, | 115546, | 240187 |
σ = 152.9 N , L = 1.124 m
|
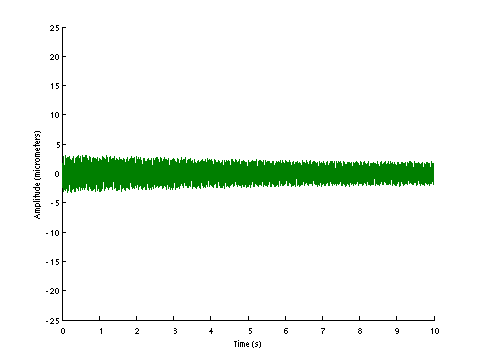 | 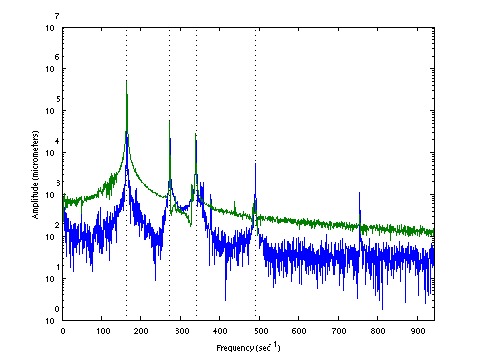 |
|
Six bead data |
|
| D0154 dataset solution |
 |
| ω | = | 98.02, | 175.93, | 305.36, | 373.85, | 398.98, | 437.94 | sec-1 |
| Λ | = | 9607, | 30951, | 93246, | 139763, | 159187, | 191790 |
σ = 166.0 N , L = 1.124 m
|
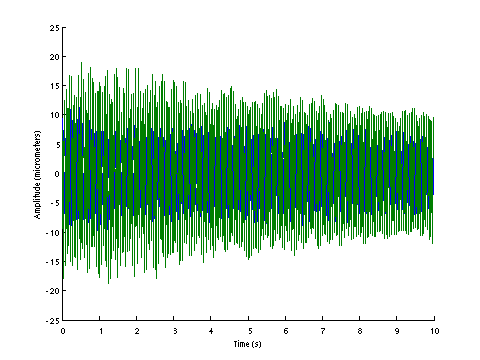 | 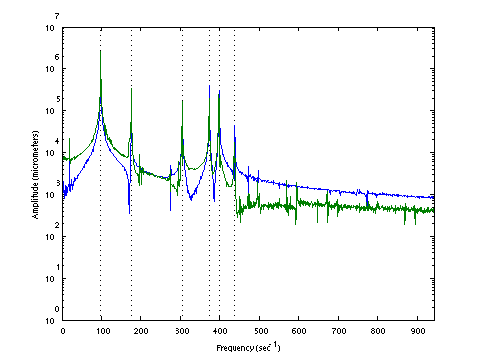 |
|
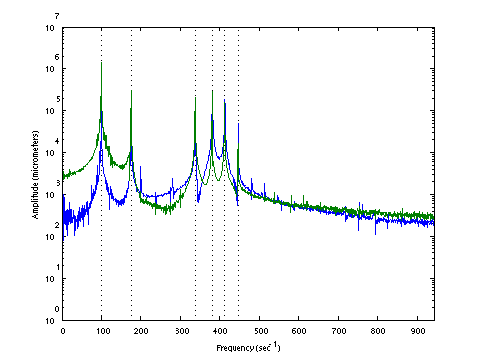
| D0158 dataset solution |
 |
| ω | = | 99.90, | 175.30, | 338.04, | 380.76, | 412.81, | 446.73 | sec-1 |
| Λ | = | 9981, | 30730, | 114268, | 144979, | 170408, | 199572 |
σ = 161.4 N , L = 1.124 m
|
 |  |
|










































