Gallery of Research
Home |
Gallery of Research |
Publications |
Personal Interests
Negative concentrations
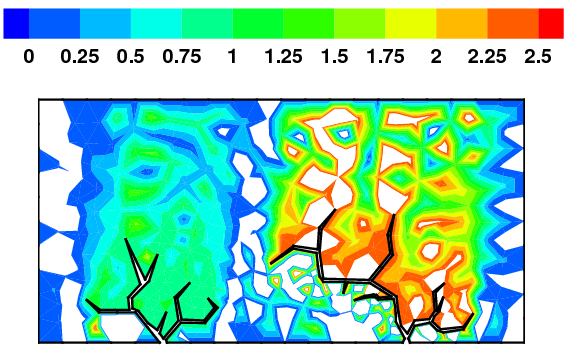
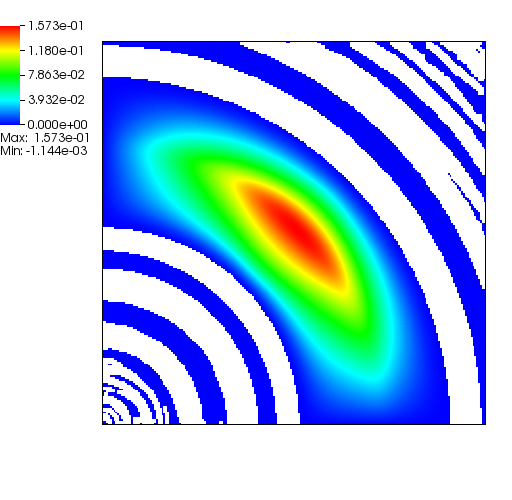
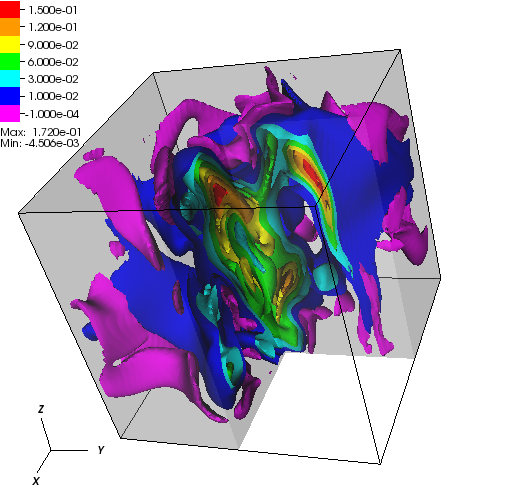
When the subsurface is highly anisotropic, many standard numerical discretizations
are unable to ensure the maximum principle. That is, negative concentrations may
arise. In the above pictorial examples, the white regions and purple contours denote
maximum principle violations in the concentration field.
High performance computing

Understanding how to optimally utilize the computational and memory resources on modern
hardware architecture is vital to achieving High Performance Computing (HPC).


A performance spectrum model is needed to understand how different hardware architectures,
software implementations, and numerical discretization can affect the
performance of complex PDE solvers.
Chromium remediation study
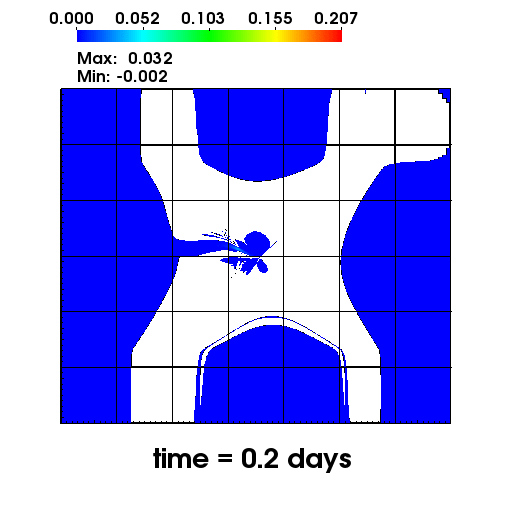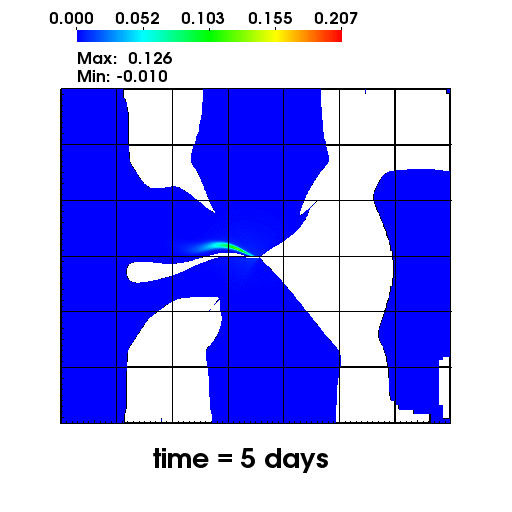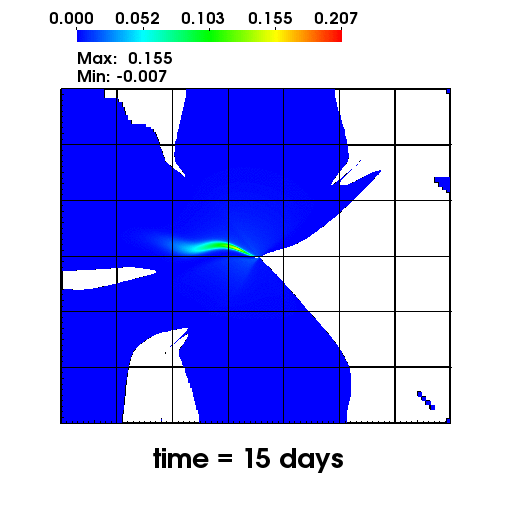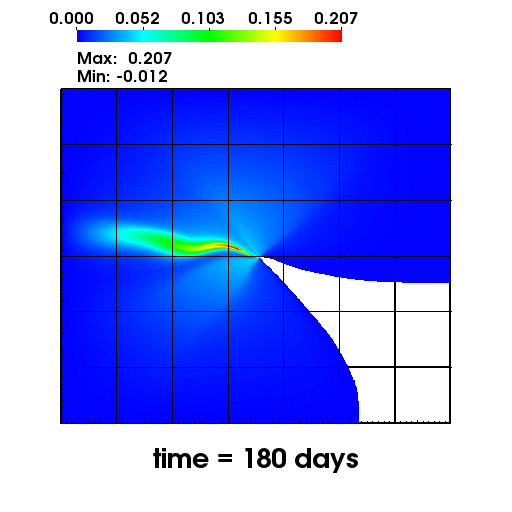
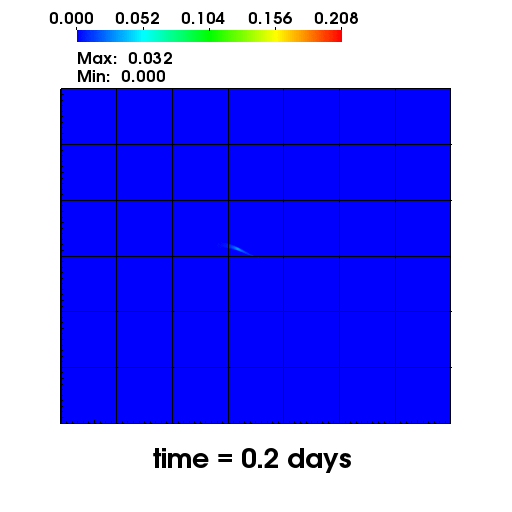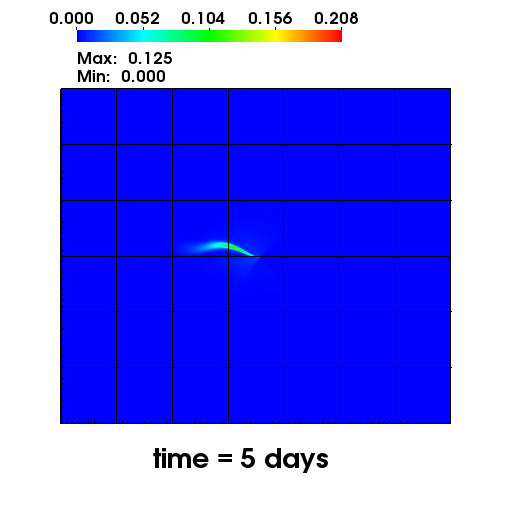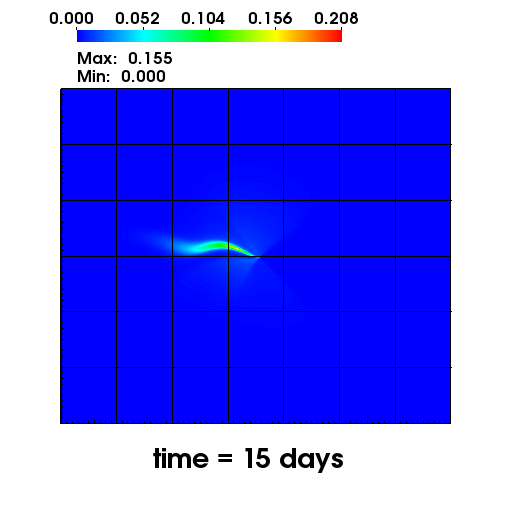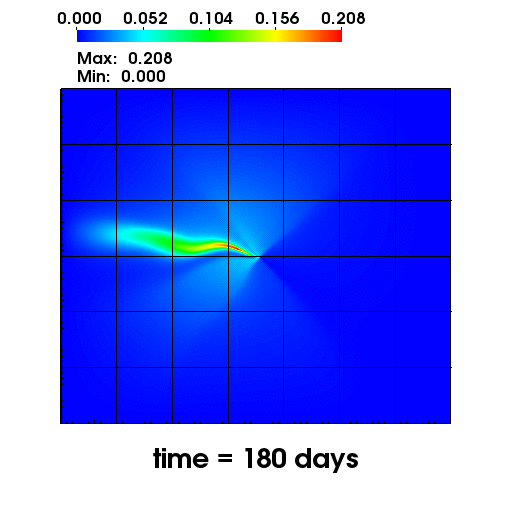
The left figure depicts the diffusion of Chromium into the Sandia Canyon when
a non-monotone numerical discretization is used to model this problem. However,
if an optimization-based computational framework is used to enforce the non-negative
constraint, the non-physical concentrations are removed as seen from the right figure.
The presense of negative concentrations not only make no physical sense but can
cause algorithmic failure in the computational framework when geochemical reactions occur.

Strong-scaling performance of the optimization-based computational framework on the AMD
Opteron (Mustang) and Intel Xeon "Ivybridge" (Wolf) HPC systems. It is
evident that parallel performance depends on the hardware architecture as well as how
its computational and memory resources are utilized.
Miscible displacement


A less viscous fluid (blue) displacees a more viscous one (red) in a highly heterogeneous
porous medium. The left figure has violations in the maximum principle, but the non-negative
computational framework eliminates such violations as seen from the right figure.


Numerical differences between the standard framework and the optimization-based framework (left)
as well as the differences between the standard framework and simply clipping off
the violating cells (right).
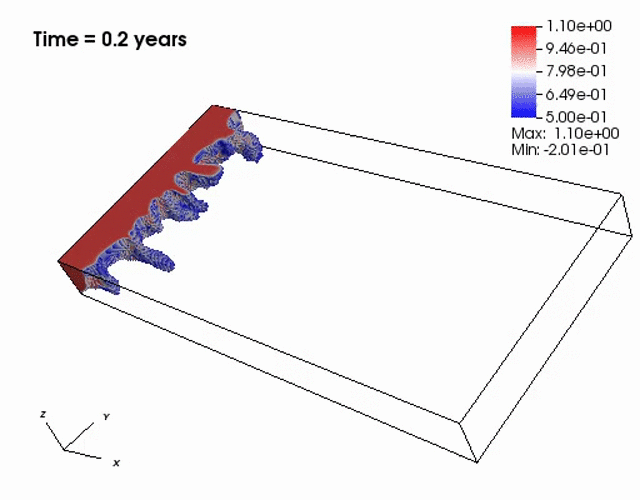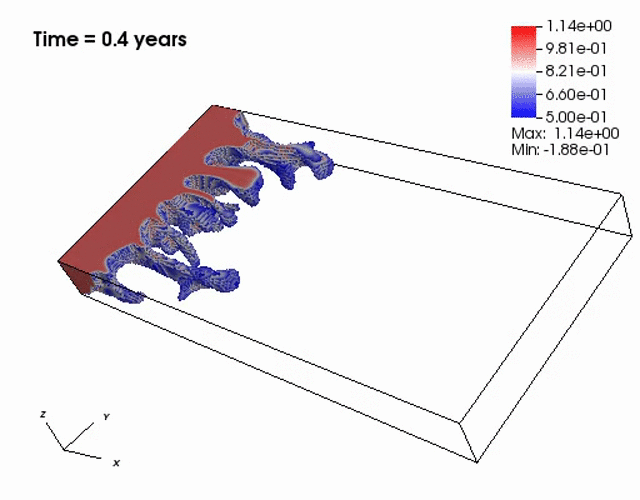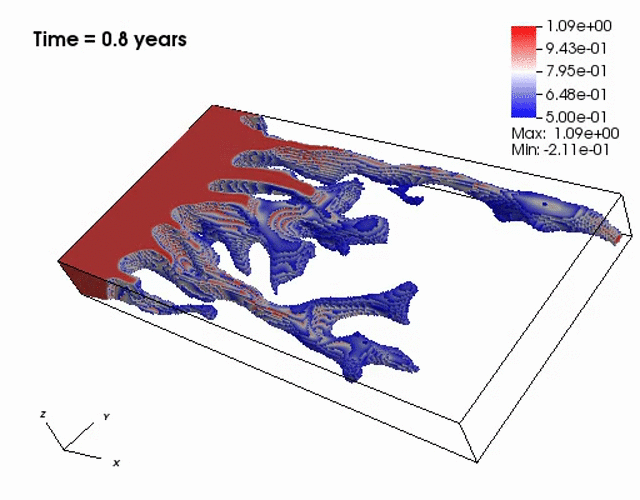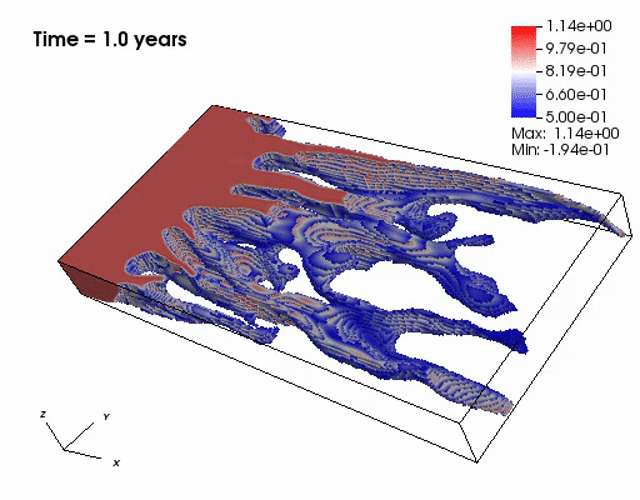
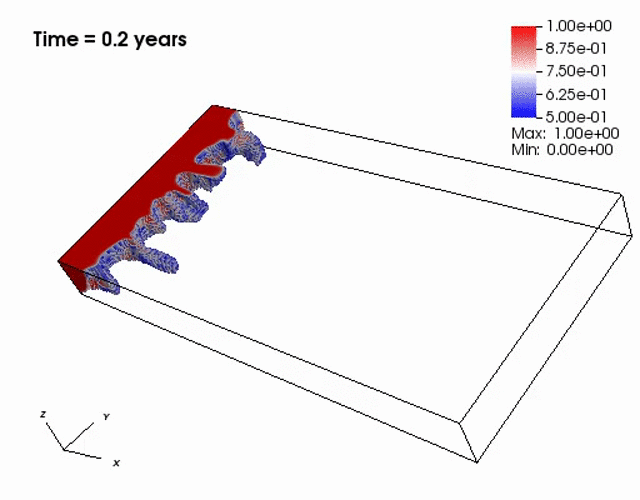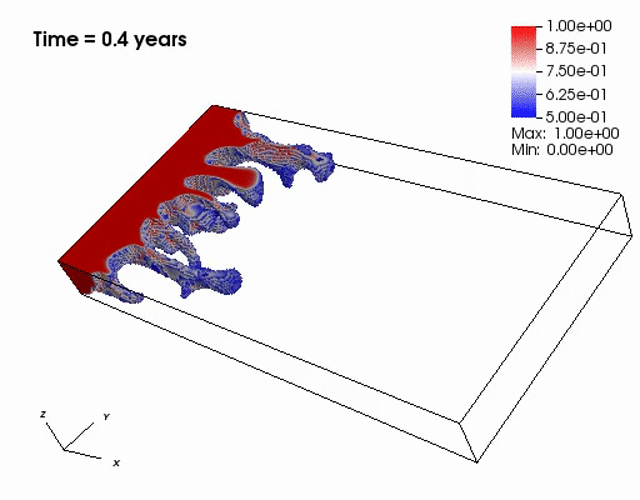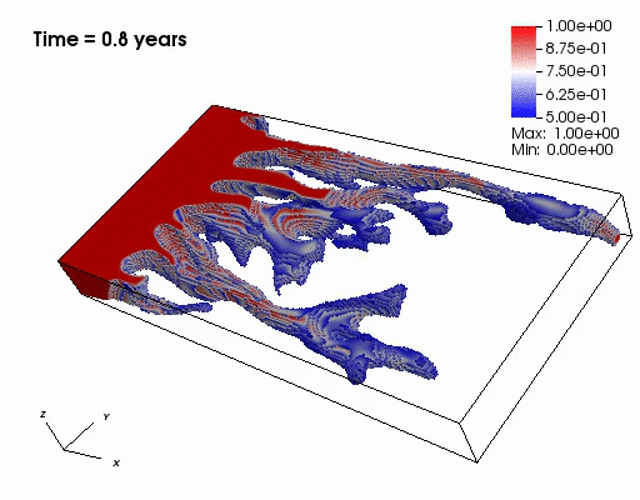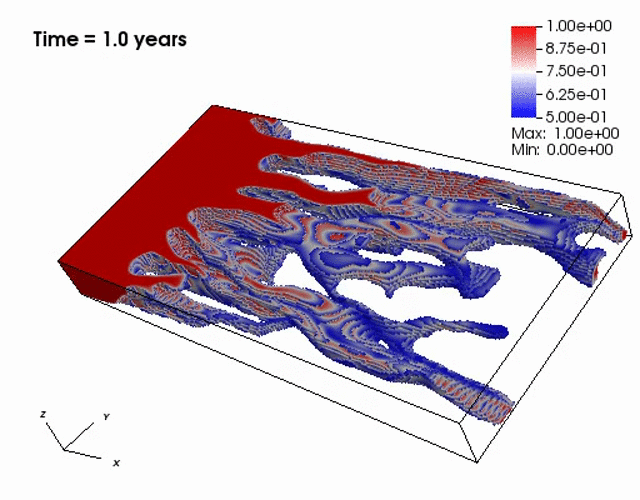
The presence of the negative concentations greatly impacts 3D simulations, especially
if a looser solver tolerance or coarse mesh is chosen.
Predicting parallel performance

Higher arithmetic intensities typically lead to better
parallel performance as more MPI processes are utilized.


A single-core "perfect-cache" roofline efficiency can predict the parallel
performance as the problem sizes increase. Both Galerkin and BLMVM have
the greatest hardware efficiencies for the smallest problems (cases
A1 through C1) but dramatically decrease for larger problems, suggesting
that linear or even superlinear speedup will be present for the largest
case studies.

A "static-scaling" plot across 256 "Ivybridge", "Haswell", and "KNL" compute nodes
(4096, 8192, and 16384 MPI processes respectively. It can be see here that KNL is
suboptimal if the problem size is too small or too large.










