Introduction
In this example, we check the correctness of SFEMaNS for a magnetic problem involving a conducting and an insulating domain. The conducting domain is splitted into two subdomains with different magnetic permeability. We consider Dirichlet boundary conditions. We use P1 finite elements for the magnetic field and P2 finite element for the scalar potential. This set up can be referred as Durand sphere in the litterature.
We solve the Maxwell equations:
\begin{align} \begin{cases} \partial_t (\mu^c \mathbf{H}) + \nabla \times \left(\frac{1}{\Rm \sigma}\nabla \times \mathbf{H} \right) = \nabla\times (\bu^\text{given} \times \mu^c \mathbf{H}) + \nabla \times \left(\frac{1}{\Rm \sigma} \nabla\times \mathbf{j} \right) & \text{in } \Omega_1, \\ \text{div} (\mu^c \mathbf {H}) = 0 & \text{in } \Omega_1 ,\\ - \partial_t \DIV (\mu^v \GRAD( \phi)) = 0 & \text{in } \Omega_2 ,\\ \bH_1 \times \bn_1 + \bH_2 \times \bn_2 = 0 & \text{on } \Sigma_\mu,\\ \mu^c_1\bH _1 \cdot \bn_1 + \mu^c_2 \bH _2 \cdot \bn_2 = 0 & \text{on } \Sigma_\mu,\\ \bH \times \bn^c + \nabla \phi \times \bn^v = 0 & \text{on } \Sigma, \\ \mu^c \bH \cdot \bn^c + \mu ^v \nabla \phi \cdot \bn^v = 0 & \text{on } \Sigma, \\ \phi = \phi_{\text{bdy}} & \text{on } \Gamma_2,\\ \bH_{|t=0}= \bH_0, \\ \phi_{|t=0}= \phi _0, \end{cases} \end{align}
in the domain \(\Omega= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in [0,10] \times [0,2\pi) \times [0,10] \; | \; r^2+z^2 \leq 100\} \). This domain is the union of a conducting domain \(\Omega_1= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in [0,1] \times [0,2\pi) \times [0,1] \; | \; r^2+z^2\leq 1\} \) and an insulating domain \(\Omega_2= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in [0,10] \times [0,2\pi) \times [0,10] \; | \; 1\leq r^2+z^2\leq 100\} \). We also set \(\Sigma= \Omega_1 \cap \Omega_2 \), \(\Gamma_1= \partial \Omega_1\setminus \Sigma \) and \(\Gamma_2= \partial \Omega_2\setminus \Sigma \) and \(\Sigma_\mu = \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in [0,1] \times [0,2\pi) \times [0,1] \; | \; r^2+z^2 = 0.5^2\} \). The variable \(\bH_1\), respectively \(\bH_2\), represents the magnetic field in the area \(\{r^2+z^2 \leq 0.5^2\} \), respectively \(\{0.5^2\leq r^2+z^2 \leq 1\} \). By analogy, we define outward normals \(\bn_1, \bn_2\) to the surface \(\Sigma_\mu\). The data are the source term \(\mathbf{j}\), the given velocity \(\bu^\text{given}\), the boundary data \(\phi_{\text{bdy}}\), the initial datas \(\bH_0\) and \(\phi _0\). The parameter \(\Rm\) is the magnetic Reynolds number. The parameter \(\mu^c\), respectively \(\mu^v\), is the magnetic permeability of the conducting region \(\Omega_1\), respectively of the vacuum region \(\Omega_2\). The parameter \(\sigma\) is the conductivity in the conducting region \(\Omega_1\).
Manufactured solutions
We approximate the following analytical solutions:
\begin{align*} H_r(r,\theta,z,t) &= \begin{cases} 0 \quad \text{if} \quad \sqrt{r^2+z^2}\leq 0.5, \\ 3 \text{capC} (\frac{a}{\sqrt{r^2+z^2}})^3 \cos(\varphi)\sin(\varphi) \quad \text{if} \quad \sqrt{r^2+z^2} > 0.5, \end{cases} \\ H_{\theta}(r,\theta,z,t) &=0, \\ H_z(r,\theta,z,t) &= \begin{cases} -\text{capA} \quad \text{if} \quad \sqrt{r^2+z^2} \leq 0.5, \\ - \text{capB} +\text{capC} (\frac{a}{\sqrt{r^2+z^2}})^3 ( 3 \cos(\varphi)^2-1) \quad \text{if} \quad \sqrt{r^2+z^2} > 0.5, \\ \end{cases}, \\ \phi(r,\theta,z,t) &= \sqrt{r^2+z^2} \cos(\varphi) - \frac{\text{capD} \cos(\varphi) a^3}{r^2+z^2}, \end{align*}
where \(\varphi\) is the polar angle of the spherical coordinate system and where \(\text{capA}, \text{capB}, \text{capC},\) and \(\text{capD}\) are defined as follows:
\begin{align*} \text{capA} &= \dfrac{-9 \mu_\max^c \mu_0}{(2\mu_\max^c\mu_0)(\mu_\max^c+2\mu_0)-2(\mu_\max^c-\mu_0)(\frac{a}{b})^3}, \\ \text{capB} &= \dfrac{(2\mu_\max^c+\mu_0)(\mu_\max^c-\mu_0)(\frac{b^3}{a^3}-1)}{(2\mu_\max^c\mu_0)(\mu_\max^c+2\mu_0)-2(\mu_\max^c-\mu_0)(\frac{a}{b})^3} , \\ \text{capC} &= \left(1-\frac{\mu_0}{\mu_\max^c} \right) \frac{\text{capA}}{3} , \\ \text{capD} &= \left(2+\frac{\mu_0}{\mu_\max^c} \right) \frac{\text{capA}}{3} , \end{align*}
with \(\mu_\max^c = \max(\mu^c)\), \(\mu_0=1\), \(a=0.5\) and \(b=1\).
We also set the given velocity field to zero.
\begin{align*} u^\text{given}_r(r,\theta,z,t) &= 0, \\ u^\text{given}_{\theta}(r,\theta,z,t) &= 0, \\ u^\text{given}_z(r,\theta,z,t) &= 0. \end{align*}
The source term \( \mathbf{j}\) is set to zero and the boundary data \(\phi_{\text{bdy}}\) is computed accordingly.
Generation of the mesh
The finite element mesh used for this test is named sphere_0.05_form.FEM. The mesh size for the P1 approximation is \(0.05\) for \(r\leq1\) and \(1\) for \(r=10\). You can generate this mesh with the files in the following directory: ($SFEMaNS_MESH_GEN_DIR)/EXAMPLES/EXAMPLES_MANUFACTURED_SOLUTIONS/sphere_0.05_form. The following images show the mesh for P1 finite elements for the conducting and vacuum regions.

Finite element mesh (P1) of the conducting region.
|
Finite element mesh (P1) of the vacuum region.
|
We note that the conducting region is the union of two domain of respective index 1 and 2. Their interface is \(r^2+z^2=0.5^2\) of index 2. It allows us to set different magnetic permeability (and also electrical conductivity) in each subregions of the conducting region.
Information on the file condlim.f90
The initial conditions, boundary conditions and the forcing term \(\textbf{j}\) in the Maxwell equations are set in the file condlim_test_6.f90. Here is a description of the subroutines and functions of interest.
-
The subroutine
init_maxwell initializes the magnetic field and the scalar potential at the time \(-dt\) and \(0\) with \(dt\) being the time step. It is done by using the functions Hexact, Phiexact as follows: Hn1 = 0.d0
Hn = 0.d0
phin1 = 0.d0
phin = 0.d0
RETURN
-
The function
Hexact contains the analytical magnetic field. It is used to initialize the magnetic field and to impose Dirichlet boundary conditions on \(\textbf{H}\times\textbf{n}\) with \(\textbf{n}\) the outter normal vector.
-
First we define the parameters \(aa, bb\) and \(\mu_0\).
REAL(KIND=8) :: aa=0.5d0, bb=1.d0, mu0=1.d0
-
If the Fourier mode m is not equal to 0, we set the magnetic field to zero.
IF (m/=0) THEN
vv = 0.d0
RETURN
END IF
-
If the the processor has no point associated to the magnetic field domain, it does nothing.
IF (SIZE(rr,2)==0) RETURN
-
We check if the number of pair of coordinates (r,z) corresponds to the number of point of the mangetic field mesh.
IF (SIZE(rr,2)/=H_mesh%np) THEN
CALL error_petsc(' BUG in Hexact')
END IF
-
We define \(\mu_\max^c\), the radial and vertical coordinates \(r, z\).
!CHAMP DURAND, H/H/phi configuration, H multi-valued at interface.
! mu1 = mu3 = mu_0 = 1
! mu2 = mu
mu = MAXVAL(mu_H_field)
r = H_mesh%rr(1,:)
-
We define the polar angle \(\varphi\) and the distance to the origin \(\rho\).
-
We define the parameters \(\text{capA}, \text{capB}, \text{capC}\) and \(\text{capD}\).
capA = -9*mu*mu0/((2*mu+mu0)*(mu+2*mu0) - 2*(mu-mu0)**2*(aa/bb)**3)
capD = (2*mu+mu0)*(mu-mu0)*((bb/aa)**3-1.d0)/((2*mu+mu0)*(mu+2*mu0) - 2*(mu-mu0)**2*(aa/bb)**3)
capC = (1.d0 - mu0/mu)*capA/3
capB = (2.d0 + mu0/mu)*capA/3
-
For the Fourier mode \(m=0\), we define the magnetic field depending of its TYPE (1 and 2 for the component radial cosine and sine, 3 and 4 for the component azimuthal cosine and sine, 5 and 6 for the component vertical cosine and sine) and the distance to the origin as follows:
DO n = 1, H_mesh%np
IF (rho(n) .LE. aa) THEN
IF (TYPE==1) THEN
vv(n) =0.d0
ELSE IF(TYPE==5) THEN
vv(n) = -capA
ELSE
vv(n) = 0.d0
END IF
ELSE
IF (TYPE==1) THEN
vv(n) = 3*capC*(aa/rho(n))**3*COS(
theta(n))*SIN(
theta(n))
ELSE IF(TYPE==5) THEN
vv(n) = -capB + capC*(aa/rho(n))**3*(3.d0*COS(
theta(n))**2-1.d0)
ELSE
vv(n) = 0.d0
END IF
END IF
END DO
-
The presence of an interface in the magnetic field, due to a discontinuity of the magnetic permeability, induces a multi-valued magnetic field on this interface. So we ensure that the magnetic field is correctly define on each sides of the interface.
DO ms = 1, H_mesh%mes !Do loop on interface, since H multi-valued
DO ns = 1, H_mesh%gauss%n_ws
n = H_mesh%jjs(ns,ms)
IF (H_mesh%i_d(H_mesh%neighs(ms)) == 1) THEN
IF (TYPE==1) THEN
vv(n) = 0.d0
ELSE IF(TYPE==5) THEN
vv(n) = -capA
ELSE
vv(n) = 0.d0
END IF
ELSE
IF (TYPE==1) THEN
vv(n) = 3*capC*(aa/rho(n))**3*COS(
theta(n))*SIN(
theta(n))
ELSE IF(TYPE==5) THEN
vv(n) = -capB + capC*(aa/rho(n))**3*(3.d0*COS(
theta(n))**2-1.d0)
ELSE
vv(n) = 0.d0
END IF
END IF
END DO
END DO
RETURN
-
The function
Phiexact contains the analytical scalar potential. It is used to initialize the scalar potential and to impose Dirichlet boundary conditions on the scalar potential.
-
First we define the parameters \(a, b\) and \(\mu_0\).
REAL(KIND=8) :: a=0.5d0, b=1.d0, mu0=1.d0
-
If the Fourier mode m is not equal to 0, we set the scalar potential to zero.
IF (m/=0) THEN
vv = 0.d0
RETURN
END IF
-
We define \(\mu_\max^c\), the radial and vertical coordinates \(r, z\) and the distance to the origin \(\rho\).
!CHAMP DURAND
mu = MAXVAL(inputs%mu_H)
r = rr(1,:)
-
We define the polar angle \(\varphi\).
DO n = 1, SIZE(rho)
IF (rho(n).LE.1.d-10) THEN
ELSE
END IF
END DO
-
We define the parameters \(\text{capA}\) and \(\text{capD}\).
capA = -9*mu*mu0/((2*mu+mu0)*(mu+2*mu0) - 2*(mu-mu0)**2*(a/b)**3)
capD = (2*mu+mu0)*(mu-mu0)*((b/a)**3-1.d0)/((2*mu+mu0)*(mu+2*mu0) - 2*(mu-mu0)**2*(a/b)**3)
-
For the Fourier mode \(m=0\), we define the scalar potential depending of its TYPE (1 for cosine and 2 for sine) and the distance to the origin.
DO n = 1, SIZE(rho)
IF (TYPE==1 .AND. rho(n).LE. (a+1.d-1)) THEN
vv(n) = -capA*rho(n)*COS(
theta(n))
ELSE IF (TYPE==1 .AND. rho(n) .GE. (b-1.d-1)) THEN
vv(n) = (rho(n)*COS(
theta(n)) - capD*COS(
theta(n))*a**3/rho(n)**2) !*(
t/t_al)**3/(1.d0+(
t/t_al)**3)
ELSE
vv(n) = 0.d0
END IF
END DO
RETURN
-
The function
Vexact is used to define the given velocity field \(\bu^\text{given}\). It is set to zero.
-
The function
Jexact_gauss is used to define the source term \(\textbf{j}\). Since \(\ROT \textbf{H}=0\), \( \bu^\text{given}=0 \) and \(\partial_t \textbf{H}=0\), we have \(\textbf{j}=0\).
-
The function
Eexact_gauss is not used in this test (no Neumann boundary conditions). So it is set to zero.
All the other subroutines present in the file condlim_test_6.f90 are not used in this test. We refer to the section Fortran file condlim.f90 for a description of all the subroutines of the condlim file.
Setting in the data file
We describe the data file of this test. It is called debug_data_test_6 and can be found in the following directory: ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
-
We use a formatted mesh by setting:
===Is mesh file formatted (true/false)?
.t.
-
The path and the name of the mesh are specified with the two following lines:
===Directory and name of mesh file
'.' 'sphere_0.05_form.FEM'
-
We use two processors in the meridian section. It means the finite element mesh is subdivised in two.
===Number of processors in meridian section
2
-
We solve the problem for \(1\) Fourier mode.
===Number of Fourier modes
1
-
We use \(1\) processor in Fourier space.
===Number of processors in Fourier space
1
-
We do not select specific Fourier modes to solve.
===Select Fourier modes? (true/false)
-
We approximate the Maxwell equations by setting:
===Problem type: (nst, mxw, mhd, fhd)
'mxw'
-
We do not restart the computations from previous results.
===Restart on velocity (true/false)
.f.
===Restart on magnetic field (true/false)
.f.
Vexact.
-
We use a time step of \(1.d10\) and solve the problem over \(1\) time iterations.
===Time step and number of time iterations
1.d10, 1
-
We approximate the Maxwell equations with the variable \(\textbf{H}\).
===Solve Maxwell with H (true) or B (false)?
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the magnetic field.
===Number of subdomains in magnetic field (H) mesh
2
===List of subdomains for magnetic field (H) mesh
1 2
-
We set the number of interface in H_mesh and give their respective labels.
===Number of interfaces in H mesh
1
===List of interfaces in H mesh
2
-
We set the number of boundaries with Dirichlet conditions on the magnetic field.
===Number of Dirichlet sides for Hxn
0
-
We set the magnetic permeability in each domains where the magnetic field is approximated.
===Permeability in the conductive part (1:nb_dom_H)
1.d0 2.d0
-
We set the conductivity in each domains where the magnetic field is approximated.
===Conductivity in the conductive part (1:nb_dom_H)
1.d0 1.d0
-
We set the type of finite element used to approximate the magnetic field.
===Type of finite element for magnetic field
1
-
We set the magnetic Reynolds number \(\Rm\).
===Magnetic Reynolds number
1.d0
-
We set stabilization coefficient for the divergence of the magnetic field and the penalty of the Dirichlet and interface terms.
===Stabilization coefficient (divergence)
1.d0
===Stabilization coefficient for Dirichlet H and/or interface H/H
1.d0
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the scalar potential.
===Number of subdomains in magnetic potential (phi) mesh
1
===List of subdomains for magnetic potential (phi) mesh
3
-
We set the number of boundaries with Dirichlet conditions on the scalar potential and give their respective labels.
===How many
boundary pieces
for Dirichlet BCs on phi?
1
===List of
boundary pieces
for Dirichlet BCs on phi
4
-
We set the number of interface between the magnetic field and the scalar potential and give their respective labels.
===Number of interfaces between H and phi
1
===List of interfaces between H and phi
3
-
We set the magnetic permeability in the vacuum domain.
===Permeability in vacuum
1.d0
-
We set the type of finite element used to approximate the scalar potential.
===Type of finite element for scalar potential
2
-
We set a stabilization coefficient used to penalize term across the interface between the magnetic field and the scalar potential.
===Stabilization coefficient (interface H/phi)
1.d0
-
We give information on how to solve the matrix associated to the time marching of the Maxwell equations.
-
===Maximum number of iterations for Maxwell solver
100
-
===Relative tolerance for Maxwell solver
1.d-6
===Absolute tolerance for Maxwell solver
1.d-10
-
===Solver type for Maxwell (FGMRES, CG, ...)
GMRES
===Preconditionner type for Maxwell solver (HYPRE, JACOBI, MUMPS...)
MUMPS
Outputs and value of reference
The outputs of this test are computed with the file post_processing_debug.f90 that can be found in the following directory: ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
To check the well behavior of the code, we compute four quantities:
-
The L2 norm of the error on the magnetic field \(\textbf{H}\).
-
The L2 norm of the error on the curl of the magnetic field \(\textbf{H}\).
-
The L2 norm of the divergence of the magnetic field \(\textbf{B}=\mu\bH\).
-
The H1 norm of the error on the scalar potential.
They are compared to reference values to attest of the correctness of the code. These values of reference are in the last lines of the file debug_data_test_6 in the directory ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC. They are equal to:
============================================
sphere_0.05_form.FEM, P1P2
===Reference results
1.09002132008650578E-002 L2 error on Hn
1.44935294860469559E-002 L2 error on Curl(Hn)
9.47173125059953824E-002 L2 norm of Div(mu Hn)
3.73975917654559026E-004 H1 error on phin
To conclude this test, we show the profile of the approximated magnetic field \(\textbf{H}\) and scalar potential \(\phi\) at the final time. These figures are done in the plane \(y=0\) which is the union of the half plane \(\theta=0\) and \(\theta=\pi\).
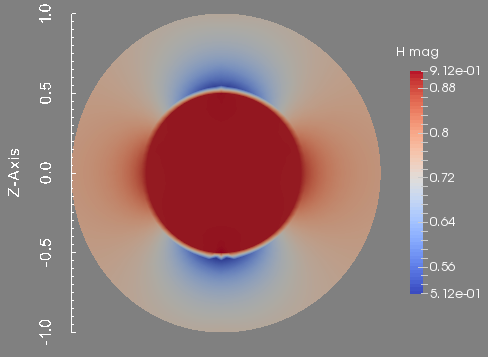
Magnetic field magnitude in the plane plane y=0.
|
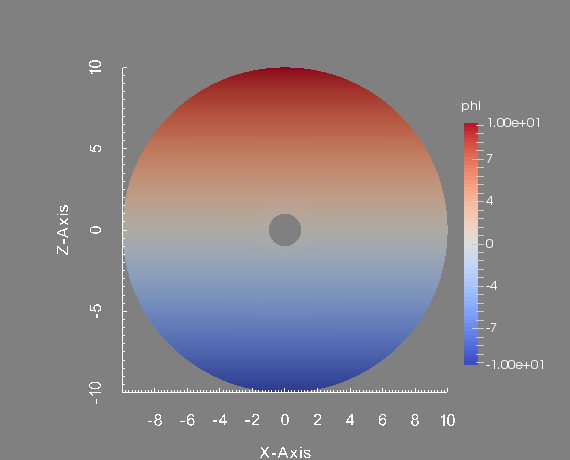
Scalar potential in the plane plane y=0.
|





