Introduction
In this example, we check the correctness of SFEMaNS for stationary magnetic problem involving a conducting with a variable magnetic permeability in (r, \(\theta\),z) and an insulating domain. The magnetic permeability in the conducting region is given. We consider Dirichlet boundary conditions. We use P2 finite elements.
We solve the Maxwell equations with the magnetic field \(\bB=\mu \bH\) as dependent variable:
\begin{align} \begin{cases} \partial_t (\mathbf{B}) + \nabla \times \left(\frac{1}{\Rm \sigma}\nabla \times( \frac{1}{\mu^c}\mathbf{B} ) \right) = \nabla\times (\bu^\text{given} \times \mathbf{B}) + \nabla \times \left(\frac{1}{\Rm \sigma} \nabla\times \mathbf{j} \right) & \text{in } \Omega_1, \\ \text{div} (\mathbf{B}) = 0 & \text{in } \Omega_1 ,\\ -\partial_t \DIV (\mu^v \GRAD( \phi)) = 0 & \text{in } \Omega_2 ,\\ \mathbf{H}\times \bn^c + \nabla \phi \times \bn^v = 0 & \text{on } \Sigma, \\ \bB \cdot \bn^c + \mu ^v \nabla \phi \cdot \bn^v = 0 & \text{on } \Sigma, \\ \phi = \phi_{\text{bdy}} & \text{on } \Gamma,\\ \bH_{|t=0}= \bH_0, \\ \phi_{|t=0}= \phi _0, \end{cases} \end{align}
in the domain \(\Omega= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in [0,10] \times [0,2\pi) \times [-10,10] \; | \; r^2+z^2 \leq 100\} \). This domain is the union of a conducting domain \(\Omega_1= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in [0,1] \times [0,2\pi) \times [-1,1]\} \) and an insulating domain \(\Omega_2\) that is the complementary of \(\Omega_1\) in \(\Omega\). We also set \(\Sigma= \Omega_1 \cap \Omega_2 \) and \(\Gamma= \partial \Omega_2\setminus \Sigma \). We define the outward normals \(\bn^c, \bn^v\) to the surface \(\Sigma\). The data are the source term \(\mathbf{j}\), the given velocity \(\bu^\text{given}\), the boundary data \(\phi_{\text{bdy}}\), the initial datas \(\bH_0\) and \(\phi _0\). The parameter \(\Rm\) is the magnetic Reynolds number. The parameter \(\mu^c\), respectively \(\mu^v\), is the magnetic permeability of the conducting region \(\Omega_1\), respectively of the vacuum region \(\Omega_2\). The parameter \(\sigma\) is the conductivity in the conducting region \(\Omega_1\).
Manufactured solutions
We define the magnetic permeability in the conducting region as follows:
\begin{align*} \mu^c(r,\theta,z)=\frac{1}{1+f_{22}(r,z)\cos(m_{22}\theta)}, \end{align*}
with \(m_{22}=4\) and
\begin{align*} f_{22}(r,z)=2^6 \frac{\text{ratio}_\mu-1}{\text{ratio}_\mu+1} \left(r(1-r)(z^2-1) \right)^3, \end{align*}
where \(\text{ratio}_\mu=50\) represents the fraction of the minimum over the maximum of the magnetic permeability in the conducting region.
Tha manufactured solutions considered in this test involve two bessel functions denoted \(BESSJ0\) and \(BESSJ1\).They are defined for any positive real argument \(x\) and satisfy the relation \( \partial_x BESSJ0 = - BESSJ1\). These functions are defined in the file bessel.f90 in the following directory: ($SFEMaNS_DIR)/FEMSUB.
We approximate the following analytical solutions:
\begin{align*} H_r(r,\theta,z,t) &= -(1+f_{22}(r,z)\cos(m_{22}\theta)) \cosh(z) BESSJ(1,r), \\ H_{\theta}(r,\theta,z,t) &=0, \\ H_z(r,\theta,z,t) &= (1+f_{22}(r,z)\cos(m_{22}\theta)) \sinh(z) BESSJ(0,r) , \\ \phi(r,\theta,z,t) &= \cosh(z) BESSJ(0,r), \end{align*}
and remind that \(\bB=\mu\bH\).
We also set the given velocity field to zero.
\begin{align*} u^\text{given}_r(r,\theta,z,t) &= 0, \\ u^\text{given}_{\theta}(r,\theta,z,t) &= 0, \\ u^\text{given}_z(r,\theta,z,t) &= 0. \end{align*}
The source term \( \mathbf{j}\) and the boundary data \(\phi_{\text{bdy}}\) are computed accordingly.
Generation of the mesh
The finite element mesh used for this test is named mesh_17_0.05.FEM. The mesh size for the P1 approximation is \(0.05\) in \(\Omega_1\) and \(0.5\) on the boundary \(\Gamma\). You can generate this mesh with the files in the following directory: ($SFEMaNS_MESH_GEN_DIR)/EXAMPLES/EXAMPLES_MANUFACTURED_SOLUTIONS/mesh_17_0.1.FEM (after editing the topology files). The following images show the mesh for P1 finite elements for the conducting and vacuum regions.
Finite element mesh (P1) of the conducting region.
|
Finite element mesh (P1) of the vacuum region.
|
Information on the file condlim.f90
The initial conditions, boundary conditions and the forcing term \(\textbf{j}\) in the Maxwell equations are set in the file condlim_test_22.f90. This condlim also uses functions of the file test_22.f90 to define the function \(f_{22}\), the magnetic permeability and its gradient. Here is a description of the subroutines and functions of interest of the file condlim_test_22.f90.
-
The subroutine
init_maxwell initializes the magnetic field and the scalar potential at the time \(-dt\) and \(0\) with \(dt\) being the time step. It is done by using the functions Hexact, Phiexact as follows: Hn1 = 0.d0
Hn = 0.d0
phin1 = 0.d0
phin = 0.d0
time=0.d0
RETURN
-
The function
Hexact contains the analytical magnetic field. It could be used to initialize the magnetic field (but not used in this test).
-
If the Fourier mode m is equal to 0, we set the magnetic field as follows.
IF (m==0) THEN
IF (TYPE==1) THEN !Bessel functions defined for reals
vv = COSH(rr(2,:))
DO n = 1, SIZE(rr,2)
vv(n) = -BESSJ1(rr(1,n))*vv(n)
END DO
ELSE IF (TYPE==5) THEN
vv = SINH(rr(2,:))
DO n = 1, SIZE(rr,2)
vv(n) = BESSJ0(rr(1,n))*vv(n)
END DO
ELSE
vv = 0.d0
END IF
-
If the Fourier mode is equal to \(m_{22}\), it is defined as follows:
ELSE IF (m==mode_mu_T22) THEN
IF (TYPE==1) THEN !Bessel functions defined for reals
vv = COSH(rr(2,:))*f_test_T22(rr(1,:),rr(2,:))
DO n = 1, SIZE(rr,2)
vv(n) = -BESSJ1(rr(1,n))*vv(n)
END DO
ELSE IF (TYPE==5) THEN
vv = SINH(rr(2,:))*f_test_T22(rr(1,:),rr(2,:))
DO n = 1, SIZE(rr,2)
vv(n) = BESSJ0(rr(1,n))*vv(n)
END DO
ELSE
vv = 0.d0
END IF
test_22.f90.
-
It is set to zero for the other Fourier modes.
ELSE
vv(:) = 0.d0
END IF
RETURN
-
The function
Phiexact contains the analytical scalar potential. It is used to impose Dirichlet boundary conditions on the scalar potential.
-
If the Fourier mode m is not equal to 0, we set the scalar potential to zero.
IF (m/=0) THEN
vv = 0.d0
RETURN
END IF
-
We define the radial and vertical coordinates \(r, z\).
-
For the Fourier mode \(m=0\), we define the scalar potential depending of its TYPE (1 for cosine and 2 for sine) as follows:
IF (TYPE==1) THEN !Bessel functions defined for reals
DO n = 1, SIZE(rr,2)
vv(n) = BESSJ0(r(n))*COSH(
z(n))
END DO
ELSE
vv = 0.d0
END IF
RETURN
-
The function
Vexact is used to define the given velocity field \(\bu^\text{given}\). It is set to zero.
-
The function
Jexact_gauss is used to define the source term \(\textbf{j}\). We remind that \( \bu^\text{given}=0 \) and \(\partial_t \textbf{H}=0\) so it is defined such that \(\textbf{j}=\ROT \bH\).
-
If the Fourier mode m is not equal to \(m_{22}\), we set the source term to zero.
IF (m/=mode_mu_T22) THEN
vv = 0.d0
RETURN
END IF
-
We define the radial and vertical coordinates \(r, z\).
-
For the Fourier mode \(m=m_{22}\), we define the source term depending of its TYPE (1 and 2 for the component radial cosine and sine, 3 and 4 for the component azimuthal cosine and sine, 5 and 6 for the component vertical cosine and sine) as follows:
dummy = f_test_T22(rr(1:1),rr(2:2))
IF (TYPE==2) THEN
vv = -(mode_mu_T22/r)*dummy(1)*BESSJ0(r)*SINH(
z)
ELSE IF (TYPE==3) THEN
vv = -dfdr_test_T22(r,
z)*BESSJ0(r)*SINH(
z)-dfdz_test_T22(r,
z)*BESSJ1(r)*COSH(
z)
ELSE IF (TYPE==6) THEN
vv = -(mode_mu_T22/r)*dummy(1)*BESSJ1(r)*COSH(
z)
ELSE
vv = 0.d0
END IF
RETURN
-
The function
mu_bar_in_fourier_space defines a stabilization term, denoted mu_bar, on the nodes or gauss points of the finite element mesh. It needs to be smaller than mu everywhere in the domain. It is done by using the function mu_bar_in_fourier_space_anal_T22 of the file test_22.f90. IF( PRESENT(pts) .AND. PRESENT(pts_ids) ) THEN
vv=mu_bar_in_fourier_space_anal_T22(H_mesh,nb,ne,pts,pts_ids)
ELSE
vv=mu_bar_in_fourier_space_anal_T22(H_mesh,nb,ne)
END IF
RETURN
-
The function
grad_mu_bar_in_fourier_space defines the gradient of mu_bar. It is done by using the function grad_mu_bar_in_fourier_space_anal_T22 of the file test_22.f90. vv=grad_mu_bar_in_fourier_space_anal_T22(pt,pt_id)
RETURN
-
The function
mu_in_real_space defines the magnetic permeability. It is done by using the function mu_in_real_space_anal_T22 of the file test_22.f90. vv = mu_in_real_space_anal_T22(H_mesh,angles,nb_angles,nb,ne)
RETURN
All the other subroutines present in the file condlim_test_22.f90 are not used in this test. We remind that the bessel function \(BESSJ0\) and \(BESSJ1\) are defined in the file bessel.f90 in the following directory: ($SFEMaNS_DIR)/FEMSUB. We refer to the section Fortran file condlim.f90 for a description of all the subroutines of the condlim file. The following describes the functions of interest of the file test_22.f90.
-
First, we define the real numbers \(\text{ratio}_\mu\), \(b\) and the integer \(m_{22}\).
REAL (KIND=8), PARAMETER, PUBLIC :: ratio_mu_T22 = 50.d0 ! the variation of mu
REAL (KIND=8), PUBLIC :: b_factor_T22 = (2**6) * (ratio_mu_T22-1.d0)/(ratio_mu_T22+1.d0)
INTEGER, PUBLIC :: mode_mu_T22 = 4
-
The function
f_test_T22 defines the function \(f_{22}\). vv = b_factor_T22*(r*(1-r)*(
z**2-1))**3
RETURN
-
The function
dfdr_test_T22 defines the r-derivative of \(f_{22}\). vv = 3 * b_factor_T22 * (
z**2-1)**3 * (r*(1-r))**2 * (1-2*r)
RETURN
-
The function
dfdz_test_T22 defines the z-derivative of \(f_{22}\). vv = 3*b_factor_T22*(r*(1-r))**3*(
z**2-1)**2*(2*
z)
RETURN
-
The function
mu_bar_in_fourier_space_anal_T22 defines stabilization term mu_bar such that it is smaller than mu everywhere in the domain. IF( PRESENT(pts) .AND. PRESENT(pts_ids) ) THEN !Computing mu at pts
r=pts(1,nb:ne)
ELSE
r=H_mesh%rr(1,nb:ne) !Computing mu at nodes
END IF
vv=1.d0/(1.d0+abs(f_test_T22(r,
z)))
RETURN
-
The function
grad_mu_bar_in_fourier_space_anal_T22 defines the gradient of mu_bar on gauss points. r(1)=pt(1)
IF (tmp(1) .GE. 0.d0 ) THEN
sign =1.0
ELSE
sign =-1.0
END IF
vv(1)=-sign*dfdr_test_T22(r(1),
z(1))/(1.d0 +abs(tmp(1)))**2
vv(2)=-sign*dfdz_test_T22(r(1),
z(1))/(1.d0 +abs(tmp(1)))**2
RETURN
-
The function
mu_in_real_space_anal_T22 defines the magnetic permeability (depending of the node in the meridian plan and its angle). DO ang = 1, nb_angles
vv(ang,:) = 1/(1+f_test_T22(H_mesh%rr(1,nb:ne),H_mesh%rr(2,nb:ne))*COS(mode_mu_T22*angles(ang)))
END DO
RETURN
Setting in the data file
We describe the data file of this test. It is called debug_data_test_22 and can be found in the following directory: ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
-
We use a formatted mesh by setting:
===Is mesh file formatted (true/false)?
.t.
-
The path and the name of the mesh are specified with the two following lines:
===Directory and name of mesh file
'.' 'mesh_17_0.05.FEM'
-
We use one processor in the meridian section. It means the finite element mesh is not subdivised.
===Number of processors in meridian section
1
-
We solve the problem for \(8\) Fourier modes.
===Number of Fourier modes
8
-
We use \(8\) processors in Fourier space.
===Number of processors in Fourier space
8
-
We do not select specific Fourier modes to solve.
===Select Fourier modes? (true/false)
-
We approximate the Maxwell equations by setting:
===Problem type: (nst, mxw, mhd, fhd)
'mxw'
-
We do not restart the computations from previous results.
===Restart on velocity (true/false)
.f.
===Restart on magnetic field (true/false)
.f.
-
We use a time step of \(1\) and solve the problem over \(10\) time iterations.
===Time step and number of time iterations
1d0, 10
-
We use the magnetic field \(\textbf{B}\) as dependent variable for the Maxwell equations.
===Solve Maxwell with H (true) or B (false)?
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the Maxwell equations.
===Number of subdomains in magnetic field (H) mesh
1
===List of subdomains for magnetic field (H) mesh
1
-
We set the number of interface in H_mesh.
===Number of interfaces in H mesh
0
-
We set the number of boundaries with Dirichlet conditions on the magnetic field.
===Number of Dirichlet sides for Hxn
0
-
The magnetic permeability is defined with a function of the file
condlim_test_22.f90. ===Is permeability defined analytically (true/false)?
.t.
-
We construct a stablization term, denoted mu_bar, on the gauss points without using its value on the nodes and a finite element interpolation.
===Use FEM Interpolation for magnetic permeability (true/false)?
.f.
-
The magnetic permeability is variable in theta.
===Is permeability variable in
theta (
true/
false)?
.t.
-
We set the conductivity in each domains where the magnetic field is approximated.
===Conductivity in the conductive part (1:nb_dom_H)
1.d0
-
We set the type of finite element used to approximate the magnetic field.
===Type of finite element for magnetic field
2
-
We set the magnetic Reynolds number \(\Rm\).
===Magnetic Reynolds number
1.d0
-
We set stabilization coefficient for the divergence of the magnetic field and the penalty of the Dirichlet and interface terms.
===Stabilization coefficient (divergence)
1.d0
===Stabilization coefficient for Dirichlet H and/or interface H/H
1.d0
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the scalar potential.
===Number of subdomains in magnetic potential (phi) mesh
1
===List of subdomains for magnetic potential (phi) mesh
2
-
We set the number of boundaries with Dirichlet conditions on the scalar potential and give their respective labels.
===How many
boundary pieces
for Dirichlet BCs on phi?
1
===List of
boundary pieces
for Dirichlet BCs on phi
3
-
We set the number of interface between the magnetic field and the scalar potential and give their respective labels.
===Number of interfaces between H and phi
1
===List of interfaces between H and phi
2
-
We set the magnetic permeability in the vacuum domain.
===Permeability in vacuum
1
-
We set the type of finite element used to approximate the scalar potential.
===Type of finite element for scalar potential
2
-
We set a stabilization coefficient used to penalize term across the interface between the magnetic field and the scalar potential.
===Stabilization coefficient (interface H/phi)
1.d0
-
We give information on how to solve the matrix associated to the time marching of the Maxwell equations.
-
===Maximum number of iterations for Maxwell solver
100
-
===Relative tolerance for Maxwell solver
1.d-6
===Absolute tolerance for Maxwell solver
1.d-10
-
===Solver type for Maxwell (FGMRES, CG, ...)
GMRES
===Preconditionner type for Maxwell solver (HYPRE, JACOBI, MUMPS...)
MUMPS
Outputs and value of reference
The outputs of this test are computed with the file post_processing_debug.f90 that can be found in the following directory: ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
To check the well behavior of the code, we compute four quantities:
-
The L2 norm of the error on the divergence of the magnetic field \(\textbf{B}=\mu\textbf{H}\).
-
The L2 norm of the error on the curl of the magnetic field \(\textbf{H}\).
-
The L2 norm of the error on the magnetic field \(\textbf{H}\).
-
The L2 norm of the error on the scalar potential.
They are compared to reference values to attest of the correctness of the code. These values of reference are in the last lines of the file debug_data_test_22 in the directory ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC. They are equal to:
============================================
mesh_17_0.05.FEM, dt=1d0, it_max=10
===Reference results
5.349471704017700E-003 !L2 norm of div(mu (H-Hexact))
8.556545587774282E-002 !L2 norm of curl(H-Hexact)
4.457274433539867E-003 !L2 norm of H-Hexact
1.179281192913028E-004 !L2 norm of phi-phiexact
To conclude this test, we show the profile of the approximated magnetic field \(\textbf{H}\) and scalar potential \(\phi\) at the final time. These figures are done in the plane \(y=0\) which is the union of the half plane \(\theta=0\) and \(\theta=\pi\).
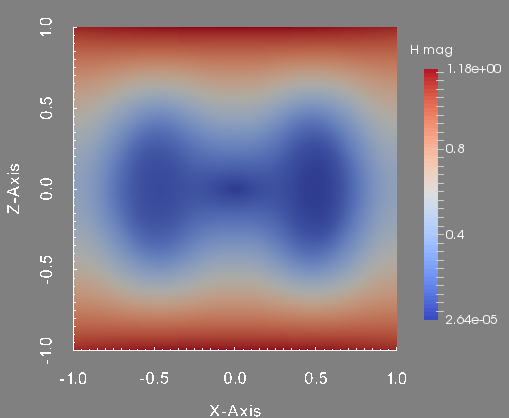
Magnetic field magnitude in the plane plane y=0.
|
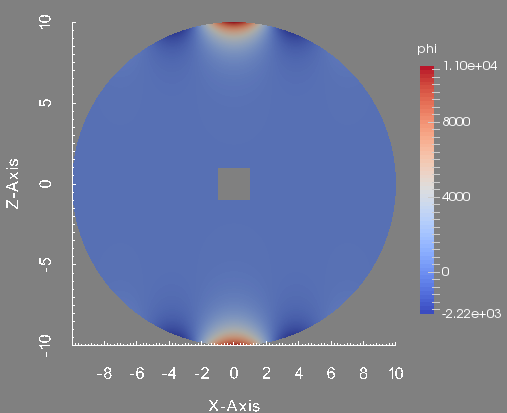
Scalar potential in the plane plane y=0.
|





