Introduction
In this example, we check the correctness behavior of SFEMaNS for a magnetohydrodynamic problem with a moving solid obstacle involving Dirichlet boundary conditions. The set up consists of a fluid driven by contra rotative impellers in a cylinder container. We also consider a two layer side walls wher the outter wall has a different electrical conductivity than the rest of the domain. Moreover, the magnetic permeability of the impeller (solid obstacle) is larger than the one of the fluid and the side walls. In the litterature, this set up is referred as Von Karman Sodium. Here we study the case with impellers called TM73, we refer to the paper Direct numerical simulation of the axial dipolar dynamo in the Von Karman Sodium experiment (Nore et al. 2016) for more information on this set up.
We note this test does not involve manufactured solutions and consists of checking four quantities, like the \(\bL^2\) norm of the magnetic field, are the same than the values of reference.
We solve the Navier-Stokes equations:
\begin{align*} \partial_t\bu+\left(\ROT\bu\right)\CROSS\bu - \frac{1}{\Re}\LAP \bu +\GRAD p &=\bef + (\ROT \textbf{H}) \times (\mu^c \textbf{H}) &\text{ in } \Omega_\text{fluid}, \\ \bu & = r \omega \be_\theta &\text{ in } \Omega_\text{imp_bot}, \\ \bu & = -r \omega \be_\theta &\text{ in } \Omega_\text{imp_top}, \\ \DIV \bu &= 0, &\\ \bu_{|\Gamma} &= \bu_{\text{bdy}} ,& \\ \bu_{|t=0} &= \bu_0, &\\ p_{|t=0} &= p_0,& \end{align*}
in the domain \(\Omega_1= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in [0,1] \times [0,2\pi) \times [-1,1]\}\). This domain is the union of a fluid domain \(\Omega_\text{fluid}\) and two solid domains, \(\Omega_\text{imp_top}\) and \(\Omega_\text{imp_bot}\) that represent the impellers. These subdomains depend of the time as the impellers are contra rotating with an angular velocity \(\omega\). We also define \(\Gamma_1 =\partial \Omega_1 \).
We solve the Maxwell equations with the magnetic field \(\bB=\mu \bH\) as dependent variable:
\begin{align*} \partial_t (\mathbf{B}) + \nabla \times \left(\frac{1}{\Rm \sigma}\nabla \times( \frac{1}{\mu^c}\mathbf{B} ) \right) & =\nabla\times (\bu^\text{given} \times \mathbf{B}) , \\ \text{div} (\mu \mathbf {H}) &= 0 ,\\ {\bH \times \bn}_{|\Gamma} &= {\bH_{\text{bdy}} \times \bn}_{|\Gamma},\\ \bH_{|t=0}&= \bH_0. \end{align*}
in the domain \(\Omega\) which is the union the of set \(\Omega_1\) and \(\Omega_2= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in [1,1.6] \times [0,2\pi) \times [-1,1]\}\). We also define \(\Gamma= \partial \Omega \) and \(\Sigma=\Omega_1 \cap \Omega_2 \). The data are the source term \(\bef\), an angular velocity \(\omega\), the penalty function \(\chi\), the boundary data \(\bu_{\text{bdy}}\), the initial datas \(\bu_0\) and \(p_0\). The parameters are the kinetic Reynolds number \(\Re\), the magnetic Reynolds numbers \(\Rm\), the magnetic permeability \(\mu\) and the conductivity \(\sigma\).
Remarks:
-
We note that the velocity field is forced to match the velocity of the impellers in the solid subdomains with a penalty method. This method involves a penalty function \(\chi\) equal to 0 in \(\Omega_\text{imp_top} \cup \Omega_\text{imp_bot}\) and 1 elsewhere.
-
To take into account a magnetic permeability variable in the azimuthal direction, we approximate the Maxwell equations with the magnetic field \(\textbf{B}=\mu\textbf{H}\) as dependent variable. We refer to the section Extension to magnetic permeability variable in time and azimuthal direction for more details of this algorithm.
Manufactured solutions
As mentionned earlier this test does not involve manufactured solutions. As a consequence, we do not consider specific source term and only initialize the variables to approximate.
The initial velocity field and pressure are initialized as follows:
\begin{align*} u_r(r,\theta,z,t) &= 0, \\ u_{\theta}(r,\theta,z,t) &= \begin{cases} -r \omega \be_\theta & \text{ in } \Omega_\text{imp_top}, \\ 0 &\text{ in } \Omega_\text{fluid}, \\ r \omega \be_\theta & \text{ in } \Omega_\text{imp_bot}, \end{cases} \\ u_z(r,\theta,z,t) &= 0, \\ p(r,\theta,z,t) &= 0, \end{align*}
The magnetic field is iniatialized as follows:
\begin{align*} H_r(r,\theta,z,t) &= 0, \\ H_{\theta}(r,\theta,z,t) &= 10^{-3}(\cos(\theta)-\sin(\theta)), \\ H_z(r,\theta,z,t) &= 10^{-3}, \end{align*}
The penalty function \(\chi\) is defined such that it is equal to 0 in \(\Omega_\text{imp_top} \cup \Omega_\text{imp_bot}\) and 1 elsewhere. We note that we use a smooth penalty function.
Generation of the mesh
The finite element mesh used for this test is named mesh_T28_0_04_04_ext3.FEM and has a mesh size of \(0.04\) for the P1 approximation. You can generate this mesh with the files in the following directory: ($SFEMaNS_MESH_GEN_DIR)/EXAMPLES/EXAMPLES_MANUFACTURED_SOLUTIONS/mesh_T28_0_04_04_ext3. The following images show the mesh for P1 finite elements for the hyodrynamic, respectively magnetic, problem.

Finite element mesh (P1) for hydrodynamic problem.
|
Finite element mesh (P1) for magnetic problem.
|
The following images show a 3D representation of the fluid domain of this VKS set up and the shape of the impellers that drive the fluid.

Fluid domain of VKS Setting.
|

Impeller TM73.
|
Information on the file condlim.f90
The initial conditions, boundary conditions, the forcing term and the penalty function are set in the file condlim_test_29.f90. Here is a description of the subroutines and functions of interest.
-
First we define many numbers at the begining of the module so that every subroutines has access to these real numbers. These numbers are used to define the penalty function, meaning the shape of the impellers, or to set the velocity and the magnetic permeability of the impellers.
-
The subroutine
init_velocity_pressure initializes the velocity field and the pressure at the time \(-dt\) and \(0\) with \(dt\) being the time step. It is done by using the functions vv_exact and pp_exact as follows: time = 0.d0
DO i= 1, SIZE(list_mode)
mode = list_mode(i)
DO j = 1, 6
!===velocity
un_m1(:,j,i) = vv_exact(j,mesh_f%rr,mode,time-dt)
un (:,j,i) = vv_exact(j,mesh_f%rr,mode,time)
END DO
DO j = 1, 2
!===pressure
pn_m2(:) = pp_exact(j,mesh_c%rr,mode,time-2*dt)
pn_m1 (:,j,i) = pp_exact(j,mesh_c%rr,mode,time-dt)
pn (:,j,i) = pp_exact(j,mesh_c%rr,mode,time)
phin_m1(:,j,i) = pn_m1(:,j,i) - pn_m2(:)
phin (:,j,i) = Pn (:,j,i) - pn_m1(:,j,i)
ENDDO
ENDDO
-
The function
vv_exact contains the analytical velocity field. It is used to initialize the velocity field and to impose Dirichlet boundary conditions on the velocity field.
-
First we set the velocity to zero.
-
We define the velocity field depending of the Fourier mode and its TYPE (1 and 2 for the component radial cosine and sine, 3 and 4 for the component azimuthal cosine and sine, 5 and 6 for the component vertical cosine and sine) as follows:
IF (type==3 .AND. m==0) THEN
DO n = 1, SIZE(rr,2)
r= rr(1,n)
z= rr(2,n)
! Are we in the Bottom propeller?
IF ( if_bottom_prop .AND. r <disk_radius .AND. z < top_of_blade_bot ) then
vv(n)=solid_vel*r
END IF
!are we in the top Propeller?
IF ( if_top_prop .AND. r <disk_radius .AND. z > bot_of_blade_top) then
vv(n)=-solid_vel*r
END IF
END DO
END IF
RETURN
-
The function
pp_exact contains the analytical pressure. It is used to initialize the pressure to zero.
-
The function
source_in_NS_momentum computes the source term \(\bef\) of the Navier-Stokes equations. It is set to zero.
-
The function
penal_in_real_space defines the penalty function \(\chi\) in the real space (depending of the node in the meridian plan and its angle n). It is done by calling the function smooth_penal_in_real_space as follows: vv=smooth_penal_in_real_space(mesh,rr_gauss,angles,nb_angles,nb,ne,time)
smooth_bottom_propeller or smooth_top_propeller.
-
The function
imposed_velocity_by_penalty is used to set a non zero velocity in the impellers.
-
First we set the empellers velocity to zero.
-
We do a loop on the node of the mesh and define the radial and vertical coordinates r, z.
DO n = 1, SIZE(rr,2)
r= rr(1,n)
z= rr(2,n)
-
If the node considered has a vertical coordinate smaller than \(-0.5\), it is in the bottom impeller of angular velocity solid_vel.
IF (z<-0.5d0) THEN
vv(n,3) = solid_vel*rr(1,n)
-
Else the node is in the top impeller of angular velocity -solid_vel.
ELSE
vv(n,3) = -solid_vel*rr(1,n)
ENDIF
END DO
RETURN
-
The subroutine
init_maxwell initializes the magnetic field at the time \(-dt\) and \(0\) with \(dt\) being the time step. It is done by using the function Hexact_init as follows: time = 0.d0
Hn1 = 0.d0
Hn = 0.d0
phin = 0.d0
phin1= 0.d0
m_max_c = SIZE(list_mode)
time = -dt
DO k=1,6
DO i=1, m_max_c
mode = list_mode(i)
Hn1(:,k,i) = Hexact_init(k, H_mesh%rr, mode, mu_H_field, time)
IF (k<3) THEN
phin1(:,k,i) = Phiexact(k, phi_mesh%rr, mode, mu_phi, time)
ENDIF
ENDDO
ENDDO
time = time + dt
DO k=1,6
DO i=1, m_max_c
mode = list_mode(i)
Hn(:,k,i) = Hexact_init(k, H_mesh%rr, mode, mu_H_field, time)
IF (k<3) THEN
phin(:,k,i) = Phiexact(k, phi_mesh%rr, mode, mu_phi, time)
ENDIF
ENDDO
ENDDO
-
THe function
Hexact_init is used to initialize the magnetic field. It is defined depending of its Fourier mode and its TYPE (1 and 2 for the component radial cosine and sine, 3 and 4 for the component azimuthal cosine and sine, 5 and 6 for the component vertical cosine and sine). vv = 0.d0
!===Constant vertical field Hz
IF (m == 0) THEN
IF (TYPE == 5) THEN
vv = 1.d-3
ENDIF
ENDIF
!===Constant horizontal field Hx
IF (m == 1) THEN
IF (TYPE == 1) THEN
vv = 1.d-3
ELSEIF (TYPE == 4) THEN
vv = -1.d-3
ENDIF
ENDIF
RETURN
-
The function
Hexact contains the analytical magnetic field. It is used to impose Dirichlet boundary conditions on \(\textbf{H}\times\textbf{n}\) with \(\textbf{n}\) the outter normal vector. It is set to zero.
-
The function
extension_velocity is used to extend the velocity in the side walls. It is set to zero.
-
The function
Jexact_gauss is used to define the source term \(\textbf{j}\) that is not used in this test. So we set it to zero.
-
The function
mu_in_real_space defines the magnetic permeability in the real space (depending of the node in the meridian plan and its angle). It uses the function penal_in_real_space and the permeability of the impellers mu_disk. vv = (1.d0 - penal_in_real_space(H_mesh,H_mesh%rr(:,nb:ne),angles,nb_angles,nb,ne,time))*(mu_disk - 1.d0 ) +1.d0
RETURN
-
The function
mu_bar_in_fourier_space defines a stabilization term, denoted mu_bar, on the nodes or gauss points of the finite element mesh. It needs to be smaller than mu everywhere in the domain.
-
First we check if the input and output are defined on Gauss points and define the the radial and vertical coordinates accordingly.
IF( PRESENT(pts) .AND. PRESENT(pts_ids) ) THEN !Computing mu at pts
r=pts(1,nb:ne)
z=pts(2,nb:ne)
ELSE
r=H_mesh%rr(1,nb:ne) !Computing mu at nodes
z=H_mesh%rr(2,nb:ne)
END IF
-
Then mu_bar is defined with the function
mu_bar_func. DO n = 1, ne - nb + 1
vv(n)=mu_bar_func(r(n),
z(n))
END DO
RETURN
-
The function
grad_mu_bar_in_fourier_space defines the gradient of mu_bar (depending on the nodes of the finite element mesh). It is done by using the function grad_mu_bar_func. vv=grad_mu_bar_func(pt(1),pt(2))
RETURN
We note that we do not describe all the functions that are called in mu_in_real_space, mu_bar_in_fourier_space and grad_mu_bar_in_fourier_space.
Setting in the data file
We describe the data file of this test. It is called debug_data_test_29 and can be found in the directory ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
-
We use a formatted mesh by setting:
===Is mesh file formatted (true/false)?
.t.
-
The path and the name of the mesh are specified with the two following lines:
===Directory and name of mesh file
'.' mesh_T28_0_04_04_ext3.FEM
-
We use one processor in the meridian section. It means the finite element mesh is not subdivised.
===Number of processors in meridian section
1
-
We solve the problem for \(64\) Fourier modes.
===Number of Fourier modes
64
-
We use \(8\) processors in Fourier space.
===Number of processors in Fourier space
8
-
We do not select specific Fourier modes to solve.
===Select Fourier modes? (true/false)
-
We approximate the MHD equations by setting:
===Problem type: (nst, mxw, mhd, fhd)
'mhd'
-
We do not restart the computations from previous results.
===Restart on velocity (true/false)
.f.
===Restart on magnetic field (true/false)
.f.
-
We use a time step of \(0.01\) and solve the problem over \(10\) time iterations.
===Time step and number of time iterations
0.01 10 !628 iterations = one turn since omega=1.0
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the Navier-Stokes equations.
===Number of subdomains in Navier-Stokes mesh
7
===List of subdomains for Navier-Stokes mesh
1 2 3 4 5 6 7
-
We set the number of boundaries with Dirichlet conditions on the velocity field and give their respective labels.
===How many
boundary pieces
for full Dirichlet BCs on velocity?
3
===List of
boundary pieces
for full Dirichlet BCs on velocity
2 10 4
-
We set the kinetic Reynolds number \(\Re\).
-
We use a penalty function function to take into account the presence of impellers.
===Use penalty in NS domain (true/false)?
.t.
-
The solid is moving (contra rotating impellers), so we need to set:
===Use nonzero velocity in solids (true/false)?
.t.
-
We give information on how to solve the matrix associated to the time marching of the velocity.
-
===Maximum number of iterations for velocity solver
100
-
===Relative tolerance for velocity solver
1.d-6
===Absolute tolerance for velocity solver
1.d-10
-
===Solver type for velocity (FGMRES, CG, ...)
GMRES
===Preconditionner type for velocity solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
We give information on how to solve the matrix associated to the time marching of the pressure.
-
===Maximum number of iterations for pressure solver
100
-
===Relative tolerance for pressure solver
1.d-6
===Absolute tolerance for pressure solver
1.d-10
-
===Solver type for pressure (FGMRES, CG, ...)
GMRES
===Preconditionner type for pressure solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
We give information on how to solve the mass matrix.
-
===Maximum number of iterations for mass matrix solver
100
-
===Relative tolerance for mass matrix solver
1.d-6
===Absolute tolerance for mass matrix solver
1.d-10
-
===Solver type for mass matrix (FGMRES, CG, ...)
CG
===Preconditionner type for mass matrix solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
We use the magnetic field \(\textbf{B}\) as dependent variable for the Maxwell equations.
===Solve Maxwell with H (true) or B (false)?
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the magnetic field.
===Number of subdomains in magnetic field (H) mesh
9
===List of subdomains for magnetic field (H) mesh
1 2 3 4 5 6 7 8 9
-
We set the number of interface in H_mesh and give their respective labels.
===Number of interfaces in H mesh
1
===List of interfaces in H mesh
10
-
We set the number of boundaries with Dirichlet conditions on the magnetic field and give their respective labels.
===Number of Dirichlet sides for Hxn
3
===List of Dirichlet sides for Hxn
2 12 4
-
The magnetic permeability is defined with a function of the file
condlim.f90. ===Is permeability defined analytically (true/false)?
.t.
-
We construct a stabilization term, denoted mu_bar, on the gauss points without using its value on the nodes and a finite element interpolation.
===Use FEM Interpolation for magnetic permeability (true/false)?
.f.
-
The magnetic permeability is variable in theta.
===Is permeability variable in
theta (
true/
false)?
.t.
-
We set the conductivity in each domains where the magnetic field is approximated.
===Conductivity in the conductive part (1:nb_dom_H)
1.d0 1.d0 1.d0 1.d0 1.d0 1.d0 1.d0 1.d0 4.5d0
-
We set the type of finite element used to approximate the magnetic field.
===Type of finite element for magnetic field
2
-
We set the magnetic Reynolds number \(\Rm\).
===Magnetic Reynolds number
5.d0
-
We set stabilization coefficient for the divergence of the magnetic field and the penalty of the Dirichlet and interface terms.
===Stabilization coefficient (divergence)
1.d1
===Stabilization coefficient for Dirichlet H and/or interface H/H
1.d1
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the scalar potential.
===Number of subdomains in magnetic potential (phi) mesh
0
-
We give information on how to solve the matrix associated to the time marching of the Maxwell equations.
-
===Maximum number of iterations for Maxwell solver
100
-
===Relative tolerance for Maxwell solver
1.d-6
===Absolute tolerance for Maxwell solver
1.d-10
-
===Solver type for Maxwell (FGMRES, CG, ...)
GMRES
===Preconditionner type for Maxwell solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
To get the total elapse time and the average time in loop minus initialization, we write:
===Verbose timing? (true/false)
.t.
lis when you run the shell debug_SFEMaNS_template.
Outputs and value of reference
The outputs of this test are computed with the file post_processing_debug.f90 that can be found in the following directory: ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
To check the well behavior of the code, we compute four quantities:
-
The L2 norm of the divergence of the velocity field divided by the H1 norm of the veloctity field.
-
The L2 norm of the divergence of the magnetic field \(\bB\) divided by the H1 norm of the magnetic field \(\bB\).
-
The L2 norm of the magnetic field \(\bB\).
-
The norm of \(\frac{1}{2}\textbf{H}\cdot\textbf{B}\) (magnetic energy).
These quantities are computed at the final time \(t=0.1\). They are compared to reference values to attest of the correctness of the code.
These values of reference are in the last lines of the file debug_data_test_29 in the directory ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC. They are equal to:
============================================
mesh_T28_0_04_04_ext3.FEM
===Reference results
2.32721482177872842E-002 !L2-norm of div of u err/norm
2.1570898796720082 !L2-norm on div of B err/norm
3.05558870563709256E-002 !L2-norm of of B
4.29583871918592472E-005 !norm 0.5*B.H
To conclude this test, we show the profile of the approximated pressure, velocity magnitude and magnetic field magnitude at the final time. These figures are done in the plane \(y=0\) which is the union of the half plane \(\theta=0\) and \(\theta=\pi\).
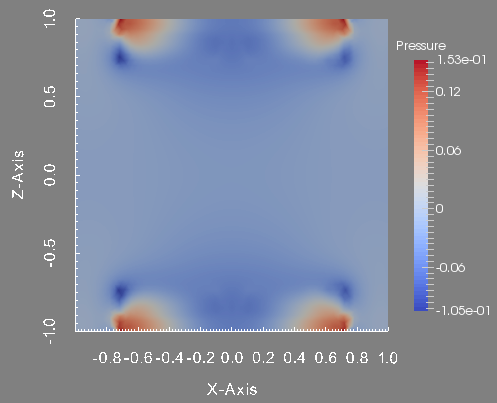
Pressure in the plane plane y=0.
|
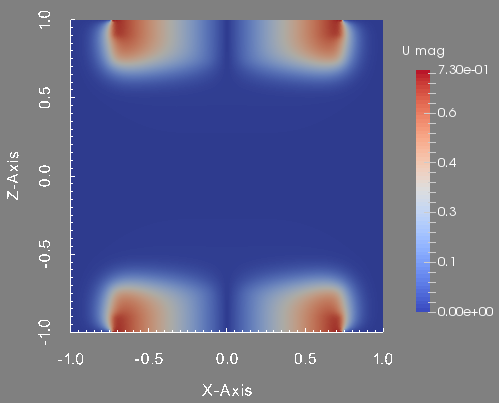
Velocity magnitude in the plane plane y=0.
|
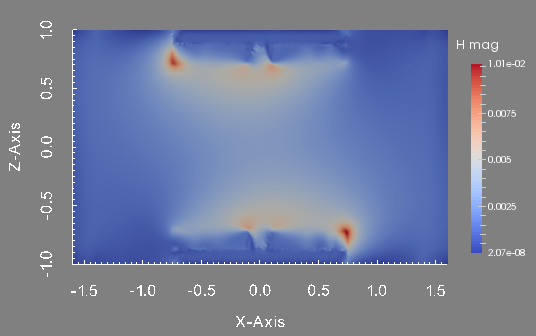
Magnetic field magnitude in the plane plane y=0.
|








