Introduction
In this example, we check the correctness of SFEMaNS for a thermohydrodynamic problem involving Dirichlet boundary conditions and periodic conditions. The fluid and solid regions do not have the same thermal diffusivity. The main difference with test 30 is that the manufactured solution is \(1\)-periodic in \(z\) so periodic conditions are used in SFEMaNS. Moreover the pressure is non null. Also, we assume that the volumetric heat capacity is uniform. In this case, it is possible to work with the thermal diffusivity instead of the volumetric heat capacity and the thermal conductivity. The heat flux continuity is still satisfied.
The domain of computation is \(\Omega= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in (0,1) \times [0,2\pi) \times (0,1)\} \). We note \(\Gamma= \partial \Omega\). It is composed of a solid and a fluid subdomain:
\begin{align*} \overline{\Omega} = \overline{\Omega_s} \cup \overline{\Omega_f}.\\ \end{align*}
The subdomains are defined followingly: \(\Omega_s = \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in (0,1/2) \times [0,2\pi) \times (0,1)\} \) and \(\Omega_f= \{ (r,\theta,z) \in {R}^3 : (r,\theta,z) \in (1/2,1) \times [0,2\pi) \times (0,1)\} \). We note \(\Gamma_f = \partial \Omega_f\).
We solve the temperature equations:
\begin{align*} \begin{cases} \partial_t T+ \tilde{\bu} \cdot \GRAD T - \DIV (\kappa \GRAD T) &= f_T, \\ T_{|\Gamma} &= T_\text{bdy} , \\ T_{|t=0} &= T_0, \end{cases} \end{align*}
in the domain \(\Omega\). The extended velocity is defined by \(\tilde{\bu} = \bu\) in \(\Omega_f\) and \(0\) in \(\Omega_s\). The diffusivity is a piecewise constant function of space: \(\kappa = \kappa_f\) in \(\Omega_f\) and \(\kappa_s\) in \(\Omega_s\), with \(\kappa_s = 10 \kappa_f\).
We solve the Navier-Stokes equations:
\begin{align*} \begin{cases} \partial_t\bu+\left(\ROT\bu\right)\CROSS\bu - \frac{1}{\Re}\LAP \bu +\GRAD p &= \alpha T \textbf{e}_z + \bef, \\ \DIV \bu &= 0, \\ \bu_{|\Gamma_f} &= \bu_{\text{bdy}} , \\ \bu_{|t=0} &= \bu_0, \\ p_{|t=0} &= p_0, \end{cases} \end{align*}
in the domain \(\Omega_f\). We denote by \(\textbf{e}_z\) the unit vector in the vertical direction.
The data are the source terms \(f_T\) and \(\bef\), the boundary data \(T_\text{bdy}\) and \(\bu_{\text{bdy}}\), the initial data \(T_0\), \(\bu_0\) and \(p_0\). The parameters are the thermal diffusivities \(\kappa_s\) and \(\kappa_f\), the kinetic Reynolds number \(\Re\) and the thermal gravity number \(\alpha\). We recall that these parameters are dimensionless.
Manufactured solutions
We approximate the following analytical solutions:
\begin{align*} T(r,\theta,z,t) & = r^2(r-r_0)^2\sin(2\pi z)(1+\cos(\theta))\cos(t), \\ u_r(r,\theta,z,t) &= -2\pi (r-r_0)^2\cos(2\pi z)(1+\cos(\theta))\cos(t), \\ u_{\theta}(r,\theta,z,t) &= 2\pi (r-r_0)^2\cos(2\pi z)(1+\cos(\theta))\cos(t), \\ u_z(r,\theta,z,t) &= \frac{r-r_0}{r} \sin(2\pi z) ((3r-r_0)(1+\cos(\theta))+(r-r_0)\sin(\theta))\cos(t), \\ p(r,\theta,z,t) &= r^3 \sin(2\pi z) \cos(\theta) \cos(t), \end{align*}
where \(r_0 = 1/2\) is the limit between solid and fluid regions. The velocity is the curl of a vector field, it is thus divergence free. As mentioned, the solution is \(1\)-periodic in \(z\).
The source terms \(f_T, \bef\) and the boundary datas \(T_\text{bdy}, \bu_{\text{bdy}}\) are computed accordingly.
Generation of the mesh
The finite element mesh used for this test is named SOLID_FLUID_10.FEM and has a mesh size of \(0.1\) for the P1 approximation (same mesh as in test 30). You can generate this mesh with the files in the following directory: ($SFEMaNS_MESH_GEN_DIR)/EXAMPLES/EXAMPLES_MANUFACTURED_SOLUTIONS/SOLID_FLUID_10. The following image shows the mesh for P1 finite elements.
Finite element mesh (P1).
|
Information on the file condlim.f90
The initial conditions, boundary conditions and the forcing terms \(\textbf{f}\) in the Navier-Stokes equations and \(f_T\) in the temperature equations are set in the file condlim_test_31.f90. Here is a description of the subroutines and functions of interest.
-
The subroutine
init_velocity_pressure initializes the velocity field and the pressure at the times \(-dt\) and \(0\) with \(dt\) being the time step. This is done by using the functions vv_exact and pp_exact as follows: time = 0.d0
DO i= 1, SIZE(list_mode)
mode = list_mode(i)
DO j = 1, 6
!===velocity
un_m1(:,j,i) = vv_exact(j,mesh_f%rr,mode,time-dt)
un (:,j,i) = vv_exact(j,mesh_f%rr,mode,time)
END DO
DO j = 1, 2
!===pressure
pn_m2(:) = pp_exact(j,mesh_c%rr,mode,time-2*dt)
pn_m1 (:,j,i) = pp_exact(j,mesh_c%rr,mode,time-dt)
pn (:,j,i) = pp_exact(j,mesh_c%rr,mode,time)
phin_m1(:,j,i) = pn_m1(:,j,i) - pn_m2(:)
phin (:,j,i) = Pn (:,j,i) - pn_m1(:,j,i)
ENDDO
ENDDO
-
The subroutine
init_temperature initializes the temperature at the times \(-dt\) and \(0\) with \(dt\) the time step. This is done by using the function temperature_exact as follows: time = 0.d0
DO i= 1, SIZE(list_mode)
mode = list_mode(i)
DO j = 1, 2
tempn_m1(:,j,i) = temperature_exact(j, mesh%rr, mode, time-dt)
tempn (:,j,i) = temperature_exact(j, mesh%rr, mode, time)
ENDDO
ENDDO
-
The function
vv_exact contains the analytical velocity field. It is used to initialize the velocity field and to impose Dirichlet boundary conditions on the velocity field.
-
The limit between fluid and solid region is defined:
REAL(KIND=8) :: r0 = 0.5d0
-
The pi parameter is defined (as in each following subroutine).
REAL(KIND=8) :: pi = 3.1415926535897932d0
-
We construct the radial and vertical coordinates r, z.
-
We define the velocity field depending of its TYPE (1 and 2 for the component radial cosine and sine, 3 and 4 for the component azimuthal cosine and sine, 5 and 6 for the component vertical cosine and sine) and of its mode m as follows:
IF (TYPE==1) THEN
IF ((m==0).OR.(m==1)) THEN
vv = -2*pi*(r-r0)**2*cos(t)*cos(2*pi*z)
ELSE
vv = 0.d0
END IF
ELSE IF (TYPE==3) THEN
IF ((m==0).OR.(m==1)) THEN
vv = 2*pi*(r-r0)**2*cos(t)*cos(2*pi*z)
ELSE
vv = 0.d0
END IF
ELSE IF (TYPE==5) THEN
IF ((m==0).OR.(m==1)) THEN
vv = (r-r0)*cos(t)*sin(2*pi*z)/r * (3*r-r0)
ELSE
vv = 0.d0
END IF
ELSE IF (TYPE==6) THEN
IF (m==1) THEN
vv = (r-r0)*cos(t)*sin(2*pi*z)/r * (r-r0)
ELSE
vv = 0.d0
END IF
ELSE
vv = 0.d0
END IF
-
The function
pp_exact contains the analytical pressure.
-
We construct the radial and vertical coordinates r, z.
-
The pressure is non null only on the cosine compound and for the first mode.
IF ((TYPE==1).AND.(m==1)) THEN
vv = r**3*sin(2*pi*z)*cos(t)
ELSE
vv = 0.d0
END IF
-
The function
temperature_exact contains the analytical temperature. It is used to initialize the temperature and to impose Dirichlet boundary condition on the temperature.
-
The limit between fluid and solid region is defined:
REAL(KIND=8) :: r0 = 0.5d0
-
We construct the radial and vertical coordinates r, z.
-
We define the temperature depending on its TYPE (1 and 2 for cosine and sine) and on its mode as follows:
IF ((TYPE==1).AND.((m==0).OR.(m==1))) THEN
vv = r**2*(r-r0)**2*sin(2*pi*z)*cos(t)
ELSE
vv = 0.d0
END IF
-
The function
source_in_temperature computes the source term \(f_T\) of the temperature equations.
-
An array kappa for the value of the diffusivity at each node must be declared.
REAL(KIND=8), DIMENSION(SIZE(rr,2)) :: vv, r, z, kappa
-
The limit between fluid and solid region is defined:
REAL(KIND=8) :: r0 = 0.5d0
-
We construct the radial and vertical coordinates r, z.
-
The kappa array is filled based on the data file. The solid diffusivity is used for the region \(r \le r_0\) and the fluid diffusivity is used in the fluid region \(r > r_0\).
DO i=1,SIZE(rr,2)
IF (r(i).LE.r0) THEN
kappa(i) = inputs%temperature_diffusivity(1)
ELSE
kappa(i) = inputs%temperature_diffusivity(2)
END IF
END DO
-
The source term \( f_T = \partial_t T+ \tilde{\bu} \cdot \GRAD T - \kappa \LAP T \) is defined in two parts. Firstly, we define the part \( \partial_t T - \kappa \LAP T \):
IF (TYPE==1) THEN
IF (m==0) THEN
vv = - (-2*((2*pi**2*r**4 + 9*r*r0 - 4*pi**2*r**3*r0 - 2*r0**2 + 2*r**2*(-4.d0 + pi**2*r0**2))*kappa*Cos(t)) &
+ r**2*(r - r0)**2*Sin(t))*Sin(2*pi*z)
ELSE IF (m==1) THEN
vv = -(-((4*pi**2*r**4 + 16*r*r0 - 8*pi**2*r**3*r0 - 3*r0**2 + r**2*(-15.d0 + 4*pi**2*r0**2))*kappa*Cos(t)) &
+ r**2*(r - r0)**2*Sin(t))*Sin(2*pi*z)
ELSE
vv = 0.d0
END IF
ELSE
vv = 0.d0
END IF
IF (TYPE==1) THEN
IF (m==0) THEN
DO i=1,size(rr,2)
IF (r(i)>r0) THEN
vv(i) = vv(i) + (-3*pi*r(i)*(r(i) - r0)**4*Cos(t)**2*Sin(4*pi*z(i)))/2.d0
END IF
END DO
ELSE IF (m==1) THEN
DO i=1,size(rr,2)
IF (r(i)>r0) THEN
vv(i) = vv(i) - 2*pi*r(i)*(r(i) - r0)**4*Cos(t)**2*Sin(4*pi*z(i))
END IF
END DO
ELSE IF (m==2) THEN
DO i=1,size(rr,2)
IF (r(i)>r0) THEN
vv(i) = vv(i) - 0.5*pi*(r(i)*(r(i) - r0)**4*Cos(t)**2*Sin(4*pi*z(i)))
END IF
END DO
END IF
END IF
-
The function
source_in_NS_momentum computes the source term \(\alpha T \textbf{e}_z+\bef\) of the Navier-Stokes equations.
-
The coefficient \(\alpha\) of the Boussinesq force is declared and the limit between fluid and solid region is defined:
REAL(KIND=8) :: alpha, r0 = 0.5d0
-
The coefficient \(\alpha\) is defined based on the data file.
alpha = inputs%gravity_coefficient
-
We construct the radial and vertical coordinates r, z.
-
We construct the first part of the source term containing the Boussinesq force \(\alpha T \be_z\) and the piece of \(\bef\) that cancels it.
IF (TYPE==5) THEN
vv = alpha*(opt_tempn(:,1,i) - temperature_exact(1,rr,mode,time))
ELSE IF (TYPE==6) THEN
vv = alpha*(opt_tempn(:,2,i) - temperature_exact(2,rr,mode,time))
ELSE
vv = 0.d0
END IF
-
The rest of the source term \( \partial_t\bu+\left(\ROT\bu\right)\CROSS\bu - \frac{1}{\Re}\LAP \bu +\GRAD p \) is then added. It depends on the TYPE (1-6) and the mode (0-2).
All the other subroutines present in the file condlim_test_31.f90 are not used in this test. We refer to the section Fortran file condlim.f90 for a description of all the subroutines of the condlim file.
Setting in the data file
We describe the data file of this test. It is called debug_data_test_31 and can be found in the directory ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
-
We use a formatted mesh by setting:
===Is mesh file formatted (true/false)?
.t.
-
The path and the name of the mesh are specified with the two following lines:
===Directory and name of mesh file
'.' 'SOLID_FLUID_10.FEM'
-
We use one processor in the meridian section. It means the finite element mesh is not subdivised.
===Number of processors in meridian section
1
-
We solved the problem for \(3\) Fourier modes.
===Number of Fourier modes
3
-
We use \(3\) processors in Fourier space.
===Number of processors in Fourier space
3
-
We approximate the Navier-Stokes equations by setting:
===Problem type: (nst, mxw, mhd, fhd)
'nst'
-
We do not restart the computations from previous results.
===Restart on velocity (true/false)
.f.
-
We use a time step of \(0.01\) and solve the problem over \(100\) time iterations.
===Time step and number of time iterations
1.d-2 100
-
We set the frequency to write restart files (for test 32).
-
We set the periodic boundaries.
-
We indicate the number of couples of periodic interfaces. In our case, there is only one, the couple of interfaces 4 (bottom) and 2 (top) There could have been a second couple if we had given a different number to the top (and bottom) boundaries of solid and fluid subdomains.
-
We indicate the interfaces of each couple, and the coordinates in the plan \((r,z)\) of the vector that joins them. The vector that joins interfaces 4 and 2 is the vector \(\be_z\).
===Indices of
periodic boundaries and corresponding vectors
4 2 0.d0 1.d0
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the Navier-Stokes equations.
===Number of subdomains in Navier-Stokes mesh
1
===List of subdomains for Navier-Stokes mesh
2
-
We set the number of boundaries with Dirichlet conditions on the velocity field and give their respective labels.
===How many
boundary pieces
for full Dirichlet BCs on velocity?
2
===List of
boundary pieces
for full Dirichlet BCs on velocity
3 5
-
We set the kinetic Reynolds number \(\Re\).
-
We give information on how to solve the matrix associated to the time marching of the velocity.
-
===Maximum number of iterations for velocity solver
100
-
===Relative tolerance for velocity solver
1.d-6
===Absolute tolerance for velocity solver
1.d-10
-
===Solver type for velocity (FGMRES, CG, ...)
GMRES
===Preconditionner type for velocity solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
We give information on how to solve the matrix associated to the time marching of the pressure.
-
===Maximum number of iterations for pressure solver
100
-
===Relative tolerance for pressure solver
1.d-6
===Absolute tolerance for pressure solver
1.d-10
-
===Solver type for pressure (FGMRES, CG, ...)
GMRES
===Preconditionner type for pressure solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
We give information on how to solve the mass matrix.
-
===Maximum number of iterations for mass matrix solver
100
-
===Relative tolerance for mass matrix solver
1.d-6
===Absolute tolerance for mass matrix solver
1.d-10
-
===Solver type for mass matrix (FGMRES, CG, ...)
CG
===Preconditionner type for mass matrix solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
We solve the temperature equation.
===Is there a temperature field?
.t.
-
We set the coefficient \(\alpha\) of Boussinesq force.
===Non-dimensional gravity coefficient
1.d0
-
We set the number of domains and their label, see the files associated to the generation of the mesh, where the code approximates the temperature equation.
===Number of subdomains in temperature mesh
2
===List of subdomains for temperature mesh
1 2
-
We set the thermal diffusivity \(\kappa\).
===Diffusivity coefficient for temperature (1:nb_dom_temp)
10.d0 1.d0
-
We set the number of boundaries with Dirichlet conditions on the velocity and give their respective labels.
===How many
boundary pieces
for Dirichlet BCs on temperature?
1
===List of
boundary pieces
for Dirichlet BCs on temperature
5
-
We set the interfaces between regions where only the temperature is solved and regions where velocity and temperature is solved. It is necessary to impose boundary conditions on the velocity at these interfaces.
===Number of interfaces between velocity and temperature only domains (for nst applications)
1
===List of interfaces between velocity and temperature only domains (for nst applications)
3
-
We give information on how to solve the matrix associated to the time marching of the temperature.
-
===Maximum number of iterations for temperature solver
100
-
===Relative tolerance for temperature solver
1.d-6
===Absolute tolerance for temperature solver
1.d-10
-
===Solver type for temperature (FGMRES, CG, ...)
GMRES
===Preconditionner type for temperature solver (HYPRE, JACOBI, MUMPS...)
MUMPS
-
To get the total elapse time and the average time in loop minus initialization, we write:
===Verbose timing? (true/false)
.t.
lis when you run the shell debug_SFEMaNS_template.
Outputs and value of reference
The outputs of this test are computed with the file post_processing_debug.f90 that can be found in: ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC.
To check the well behavior of the code, we compute four quantities:
-
The L2-norm of error on u divided by the L2-norm of u exact.
-
The L2-norm of error on p divided by L2-norm of p exact.
-
The L2-norm of error on T divided by L2-norm of T exact.
-
The H1-norm of error on T divided by H1-norm of T exact.
These quantities are computed at the final time \(t=1\). They are compared to reference values to attest of the correct behavior of the code. These values of reference are in the last lines of the file debug_data_test_31 in ($SFEMaNS_DIR)/MHD_DATA_TEST_CONV_PETSC. They are equal to:
============================================
(SOLID_FLUID_10.FEM)
===Reference results
3.62826303642297190E-004 L2-norm of error on u / L2-norm of u exact
6.14657128003004566E-002 L2-norm of error on p / L2-norm of p exact
2.89730290396371859E-004 L2-norm of error on T / L2-norm of T exact
1.76053671011184849E-003 H1-norm of error on T / H1-norm of T exact
To conclude this test, we display the profile of the approximated, pressure, velocity magnitude and temperature at the final time. These figures are done in the plane \(y=0\) which is the union of the half plane \(\theta=0\) and \(\theta=\pi\).
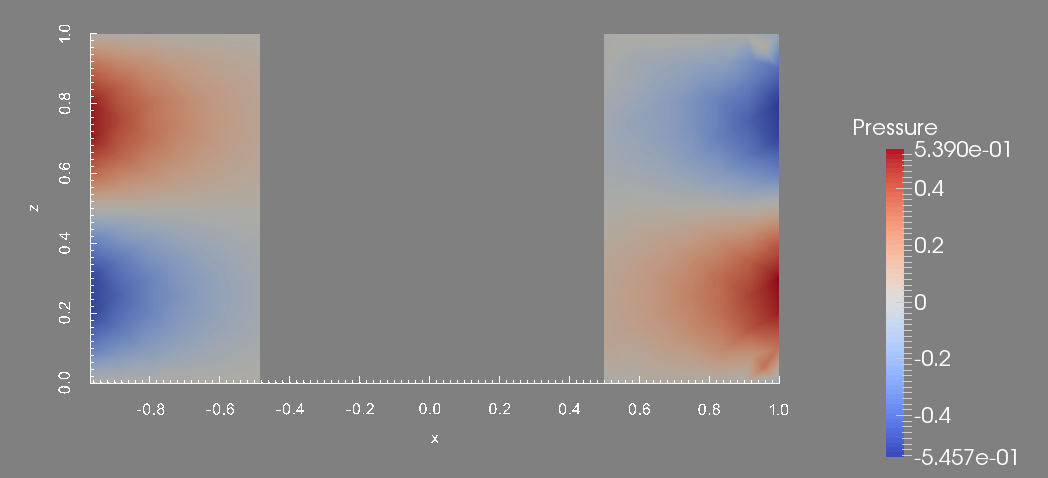
Pressure in the plane y=0.
|
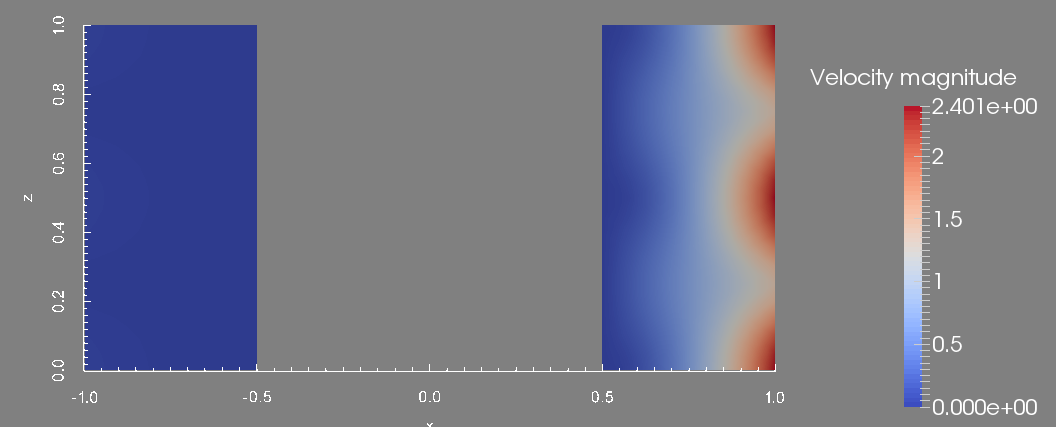
Velocity magnitude in the plane y=0.
|
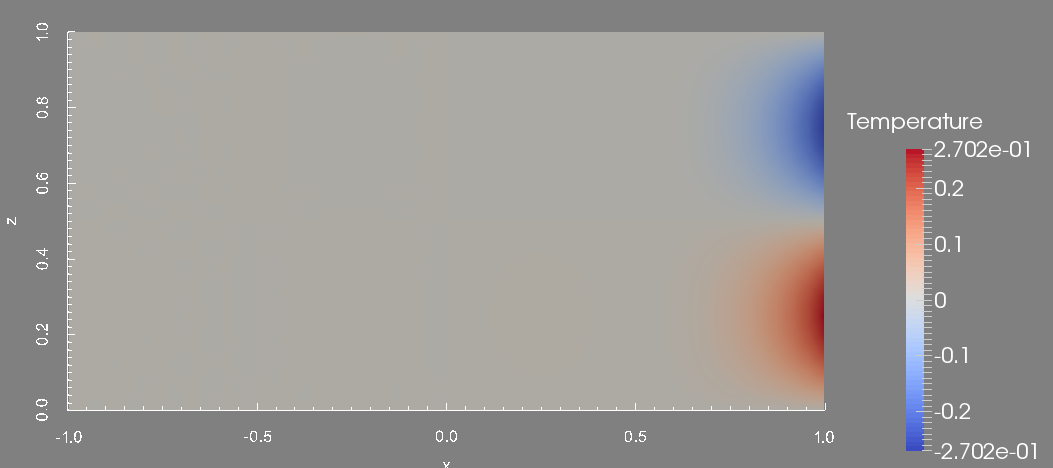
Temperature in the plane y=0.
|





