Electrostatics and Classical Density Functional Theory for Biological Systems
|
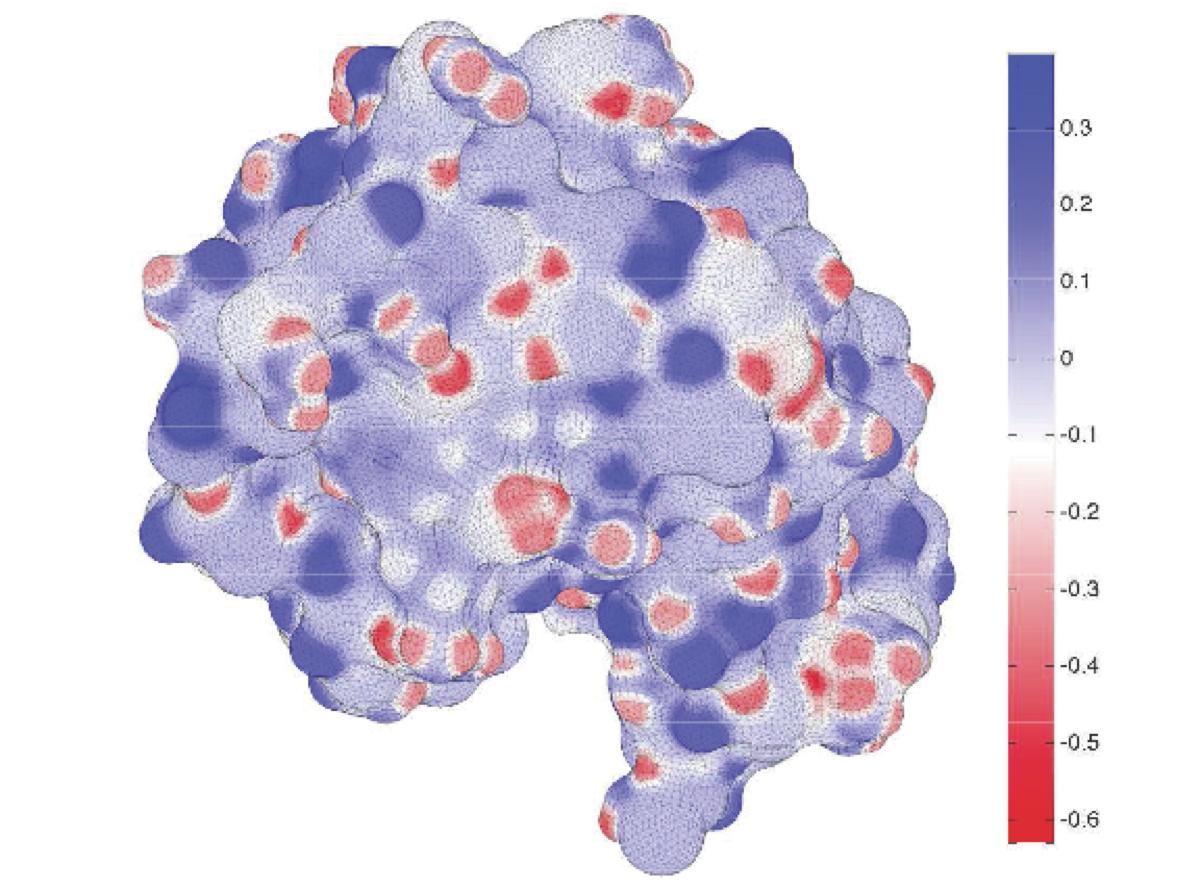
Electrostatic interactions play an essential role in the structure and function of biomolecules (proteins, DNA, cell membranes, etc.). One of the most challenging aspects for understanding these interactions is the fact that biologically active molecules are almost always in solution---that is, they are surrounded by water molecules and dissolved ions. These solvent molecules add many thousands or even millions more degrees of freedom to any theoretical study, many of which are of only secondary importance for investigations of interest. Therefore, we model the solvent using a discontinuous dielectric coefficient, and solve the Poisson equation directly using a boundary-integral formulation and the boundary-element method, BEM, to determine the induced charge distribution on the molecular surface which accounts for the change in polarization charge across the dielectric boundary. I am collaborating with Jay Bardhan to develop a comprehensive computational platform for solvation modeling, and we are developing both analytical and numerical tools as part of this effort. We are refining the BIBEE approximation algorithm for electrostatics problems with discontinuous dielectric coefficient in complex geometries. BIBEE approximates the operator arising from a boundary integral discretization of the Poisson equation, giving rigorous upper bounds and effective lower bounds for the solvation energy. We have also recently proposed a models for charge asymmetry and dielectric saturation. In addition, we are developing open source software for both finite element and boundary element solution of these problems. |
|
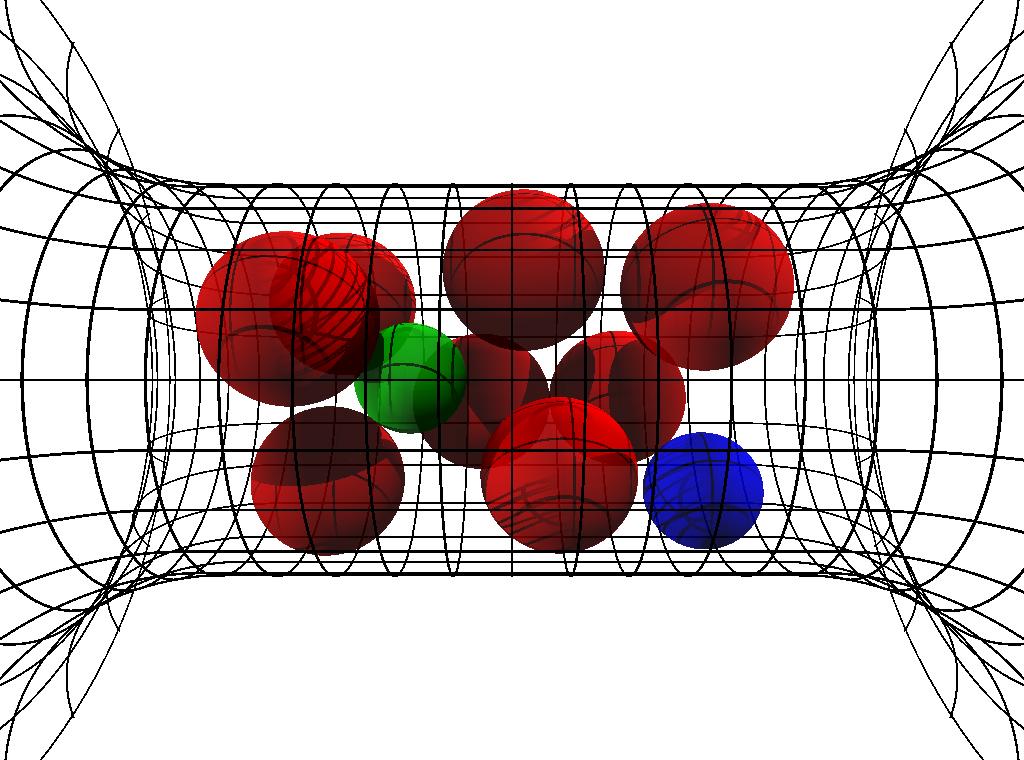
I am collaborating with Dirk Gillespie and Robert Eisenberg at Rush University Medical Center on the modeling of biological ion channels using classical Density Functional Theory of fluids. Since its inception 30 years ago, classical density functional theory (DFT) of fluids has developed into a fast and accurate theoretical tool to understand the fundamental physics of inhomogeneous fluids. To determine the structure of a fluid, DFT minimizes a free energy functional of the fluid density by solving the Euler-Lagrange equations for the inhomogeneous density profiles of all the particle species When solving on a computer, the density can be discretized (called free minimization) or a parameterized function form such as Guassians can be assumed (called parameterized minimization). This approach has been used to model freezing, electrolytes, colloids, and charged polymers in confining geometries and at liquid-vapor interfaces. DFT is different from direct particle simulations where the trajectories of many particles are followed over long times to compute averaged quantities of interest (e.g., density profiles). DFT computes these ensemble-averaged quantities directly. However, developing an accurate DFT is difficult and not straightforward. In fact, new, more accurate DFTs are still being developed for such fundamental systems as hard-sphere fluids, electrolytes, and polymers. Our group has already applied one dimensional DFT to biological problems involving ion channel permeation, successfully matching and predicting experimental data. We have extended this to 3D using efficient numerical schemes for functional evaluation and nonlinear system solution. |
Papers
- In this paper, we show that charge-sign-dependent asymmetric hydration can be modeled accurately using linear Poisson theory but replacing the standard electric-displacement boundary condition with a simple nonlinear boundary condition. Using a single multiplicative scaling factor to determine atomic radii from molecular dynamics Lennard-Jones parameters, the new model accurately reproduces MD free-energy calculations of hydration asymmetries for monatomic ions, titratable amino acids in both their protonated and unprotonated states, and some artifical test problems computed with MD. Remarkably, the model also justifies the use of linear response expressions for charging free energies. Our boundary-element method implementation demonstrates the ease with which other continuum-electrostatic solvers can be extended to include asymmetry.
- We have written a paper showing that the BIBEE approximation provides a rigorous upper bound on the solvation energy, and also a practical lower bound which is guaranteed for some convex geometries. The importance of electrostatic interactions in molecular biology has driven extensive research toward the development of accurate and efficient theoretical and computational models. Linear continuum electrostatic theory has been surprisingly successful, but the computational costs associated with solving the associated partial differential equations (PDEs) preclude the theory's use in most dynamical simulations. Modern generalized-Born models for electrostatics can reproduce PDE-based calculations to within a few percent and are extremely computationally efficient but do not always faithfully reproduce interactions between chemical groups. Recent work has shown that a boundary-integral-equation formulation of the PDE problem leads naturally to a new approach called boundary-integral-based electrostatics estimation (BIBEE) to approximate electrostatic interactions. In the present paper, we prove that the BIBEE method can be used to rigorously bound the actual continuum-theory electrostatic free energy. The bounds are validated using a set of more than 600 proteins. Detailed numerical results are presented for structures of the peptide met-enkephalin taken from a molecular-dynamics simulation. These bounds, in combination with our demonstration that the BIBEE methods accurately reproduce pairwise interactions, suggest a new approach toward building a highly accurate yet computationally tractable electrostatic model.
- This paper with Jay provides precise characterization (and improvement) of the BIBEE approximation for spherical inclusions. It is based on Kirkwood's solution using spherical harmonics. The really cool part is that we are able to characterize the BIBBE approximation as a deformation of the boundary condition at the surface. This allows us to analyze the various BIBEE schemes and compare them to Generalized Born (and leads directly to the work in here!). On our tests with a big bunch of proteins, we get the solvation energies within a few percent.
- This paper with Jay introduces expansions in ellipsoidal harmonics to solve problems in potential theory, notably determining the solvation energy of proteins. We derive things step-by-step and have lots of good references. The code repository is here.
- We have written a paper describing our scheme for solving 3D classical DFT problems for ion channel systems using a Fourier approach. We present an efficient numerical scheme for fluids of charged, hard spheres that uses \(\mathcal{O}(N \log N)\) operations and \(\mathcal{O}(N)\) memory, where \(N\) is the number of grid points. This system-size scaling is significant because of the very large \(N\) required for three-dimensional systems. The algorithm uses fast Fourier transforms (FFT) to evaluate the convolutions of the DFT Euler-Lagrange equations and Picard (iterative substitution) iteration with line search to solve the equations. For the hard-sphere DFT we use Fundamental Measure Theory. For the electrostatic DFT we present two algorithms. One is for the bulk-fluid functional of Rosenfeld [Y. Rosenfeld, 1993] that uses \(\mathcal{O}(N \log N)\) operations. The other is for the reference fluid density (RFD) functional [D. Gillespie et al., 2002]. This functional is significantly more accurate than the bulk-fluid functional, but the RFD algorithm requires \(\mathcal{O}(N^2)\) operations.
- In this paper, we developed an efficient method to calculate a high-dimensional (6d) contraction with a lot of memory reuse. This kind of operation arose in the computation of a nonlinear averaging operation used in Classical DFT for biological systems. In particular, this calculates the reference density in the RFD method of Dirk Gillespie.
- This paper demonstrates an efficient algorithm for computing the electrostatic screening integral in classical DFT. We have improved the RFD screening computation from O(N^2) to O(N log N) operations.
Software
- Ellipsoidal Potential Theory contains both a MATLAB and Python implementation of ellipsoidal harmonic expansions for solving problems of potential theory using separation of variables.
- The DFT development repository