Fracture Mechanics
|
I am collaborating with Blaise Bourdin to produce a scalable code to simulate fracture mechanics. In the area of brittle fracture, there has seen tremendous progress over the recent years, but some issues remain problematic. The most widely accepted theories, based on Griffith's criterion, are limited to the propagation of an isolated, pre-existing crack along a given path. Extending Griffith's theory into a global minimization principle, while preserving its essence, the concept of energy restitution in between surface and bulk terms, G. Francfort and J.-J. Marigo proposed a new formulation for the brittle fracture problem, capable of predicting the creation of new cracks, their path, and their interactions, in two and three space dimensions. The essence of this model is the global minimization over all crack sets \(K\) and all admissible displacement
fields \(u\) of an energy similar to
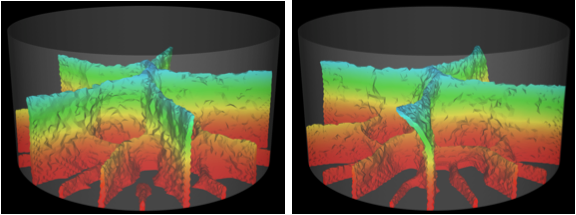
Below, I have embedded some videos of our largest runs to date. This simulates thermal fracture arising from Newtonian cooling. It is fully three dimensional, use 24M elements, and runs on 2400 processors of LoneStar at TACC. The full simulation was completed in just 6 hours. |