Friday, May 29, 2008
8:15 am to 8:30 pm (details below)

Location: Duncan Hall on the Rice University campus.  See an interactive campus map here.  For those of you non-Rice attendees who are driving to campus, parking and driving instructions are now available on the Parking page.  We will be providing a shuttle to and from campus for those of you staying in the Hilton Houston Post Oak hotel.

The day's talks will be held in McMurtry Auditorium, breaks and meals will be in Martel Hall (a large open area next to the auditorium), and the late-afternoon reception will be on Duncan Hall's front portico. Overflow for the evening banquet will be in room DH3092, a (large, open dining room on the third floor, above the auditorium).

This program would not have been possible without the sponsorship of the Rice University Computational and Applied Mathematics Department, the Dean of Engineering, the Ken Kennedy Institute, and the Empowering Leadership Alliance.

Arlie Petters – "Is there a 5th Dimension?"
       Abstract - Einstein's theory assumes that space has three dimensions --length, width, and height. Could there be an extra dimension to physical space? If so, how would we know it is there? If true, this provocative idea would profoundly impact our perception of the natural world, analogous to how we no longer think of the earth as flat. The talk will address this intriguing issue through the geometric gravitational action of tiny black holes on light.

Tony Chan – "From TV-L1 Model to Convex & Fast Optimization Models for Image & Geometry Processing" (joint work with Xavier Bresson, UCLA)
       Abstract - A "classical" model for image denoising is the TV-L2 model, in which regularity is controlled by total variation and data fidelity is measured by the L2 norm. Recently, it has been recognized that a corresponding TV-L1 model has particularly attractive features and thus have received much study. The TV-L1 model not only possesses robust constrast-invariant properties, but it also leads to the convexification of several non-convex image processing models, making them less sensitive to initial guesses and faster to minimize. In this talk, we will review some of the recent developments in this area. We show how to convexify non-convex optimization problems including shape regularization, image segmentation, classification defined on an arbitrary graph, and the level set method in the context of free boundary problems. Another important advantage of using convex optimization models is to provide fast algorithms. We introduce continuous optimization algorithms based on operator spitting, which reveal to be faster than graph-cut combinatorial optimization techniques.

Mary Wheeler – "Computational Environments for Coupling Multiphase Flow, Transport, and Geomechanics in Porous Media "
       Abstract - Cost-effective management of remediation of contamination sites and carbon sequestration in deep saline aquifers is driving the development of a new generation of subsurface simulators. The central challenge is to minimize costs of cleanup and/or maximize economic benefits from an environment whose properties are only poorly known and in which a variety of complex chemical and physical phenomena take place. In meeting this challenge we discuss possible approaches in the development of a simulator comprised of coupled programs based on high fidelity algorithms that accurately model multi-component, multi-scale, multi-phase flow and transport through porous media. In addition, this computational environment needs to account for uncertainty and include parameter estimation and optimal control capabilities.

George Papanicolaou – "Feedback Effects in Financial Markets"
       Abstract - I will discuss the effects of several kinds of traders on the volatility of equities markets: portfolio optimizers, hedgers, large movements, etc.

Don Goldfarb – "Row by Row Methods for Semidefinite Programming"
       Abstract - We present a row-by-row (RBR) method for solving semidefinite programming (SDP) based on relaxing the $n$-dimensional positive semidefinite constraint on the matrix $X$. By fixing any $(n-1)$-dimensional principal submatrix of $X$ and using its (generalized) Schur Complement, the positive semidefinite constraint is reduced to a simple second-order cone constraint. When the RBR method is applied to solve the maxcut SDP relaxation, the optimal solution of the RBR subproblem only involves a single matrix-vector product which leads to a powerful approximate method. To handle linear constraints in generic SDP, we use an augmented Lagrangian function approach. Specialized versions are presented for the maxcut SDP relaxation and the matrix completion problem since closed-form solutions for the RBR subproblems are available. Convergence properties of our augmented Lagrangian method are also studied.
       Finally, numerical results on the maxcut SDP relaxation and matrix completion problems are presented to demonstrate the robustness and efficiency of our algorithm.
       This is joint work with Zaiwen Wen, Shiqian Ma and Katya Scheinberg

Bill Cook – "Exact Solutions in Linear and Integer Programming"
       Abstract - Numerous practical computational problems are formulated as instances of linear or mixed-integer programming. Solution software for these models uses floating-point arithmetic and inexact linear algebra to obtain good approximate results. Although such solutions are satisfactory in many applications, accuracy can be important in some practical and theoretical settings. An important example is the heavy use of linear programming in Hales' proof of the Kepler Conjecture concerning the packing of spheres in three dimensions. We treat the problem of finding exact rational solutions to linear and mixed-integer programming models, including a computational study of solution methods for systems of rational linear equations. This talk is based on joint work with David Applegate, Sanjeeb Dash, Daniel Espinoza, Ricardo Fukasawa, Marcos Goycoolea, and Dan Steffy.

Alan Newell – "Phyllotaxis and Patterns on Plants"
      Abstract - Understanding why and how it is that flowers and plants arrange their phylla (the leaves, stickers, bracts) near their shoot apical meristems has challenged and intrigued natural scientists for over four hundred years. Of particular interest is the fact that the phylla arrange themselves to lie on families of spirals and the numbers of arms in each family are ennumerated by Fibonacci sequences. I will briefly describe recent attempts to understand what is observed.

Michael Trosset – "Fixed Point Methods for Embedding Large Graphs"
       Abstract - Manifold learning is a collection of unsupervised machine learning techniques for nonlinear dimension reduction. Many popular manifold learning techniques can be described in three steps:
    (1) represent multivariate data as a graph,
    (2) use the graph to compute dissimilarities between pairs of vertices, and
    (3) embed the dissimilarities in a low-dimensional Euclidean space.

Step (3) is sometimes called multidimensional scaling (MDS), for which a number of algorithms are available. Research in manifold learning has emphasized spectral embedding methods (classical MDS), partly because it is thought that alternative methods involving numerical optimization are prohibitively expensive.

Kruskal's (1964) raw stress criterion is the sum of the squared errors between the dissimilarities and the embedded Euclidean distances that approximate them. It must be minimized by numerical optimization, e.g., Newton's method. However, specialized algorithms exist that decrease stress by relatively inexpensive transformation of the current configuration. These methods are slow to converge, but they have good global properties and tend to produce reasonable configurations in a few iterations---at far less expense than matrix factorization. I will describe the Diagonal Majorization Algorithm, proposed by Trosset and Groenen (2005), and apply it to several embedding problems.

Footnote: This talk also provides a counterpoint to the point of Kearsley, Tapia, and Trosset (1998), "The solution of the metric stress and sstress problems in multidimensional scaling by Newton's method."

Rodrigo Banuelos – "Heat Asymtotics for L\'evy Processes"
       Abstract - We recall some of the well known results on the asymptotics of the trace of the heat semigroup for the Dirichlet Laplacian. We then address similar questions for fractional and relativistic Laplacians. The latter are pseudo differential operators associated with L\'evy processes and this is our point of view in our investigations.

Florian Potra – "Polynomial Complexity vs. Superlinear Convergence"
       Abstract - Interior point methods have revolutionized the field of mathematical programming over the past three decades. They have been used for proving polynomial complexity for different classes of mathematical programming problems, and they have been implemented in very efficient software packages for solving large scale optimization problems arising in a variety of applications. While the implemented interior point methods may not always have proven computational complexity, they typically posses superlinear convergence. The talk highlights the most relevant results on the polynomial complexity and superlinear convergence of interior point methods in the literature, and presents some recent results obtained by the speaker and his collaborators.

Carlos Castillo-Chavez – "Epidemics and Prejudice: The Case of Influenza, HIV and Related Diseases"
       Abstract - In 1986 HIV risk was defined often by nationality (Haitian), or by sexual preference, or by economic condition (being poor). The current flu outbreaks have made Mexicans undesirable individuals at many places including at unexpected nations like Haiti or Peru. I became interested in the study of HIV when I realized that in modeling human interactions (social dynamics) the role of the investigator was never that of a passive observer but in fact that of an active participant, sort of a pre-decision maker. It seemed obvious that researchers often decide a priori who is and who is not at risk of a disease or who poses or does not pose a risk to the health of others. These subjective decisions impact the way we model the world. They can play a critical role in the construction of highly heterogenous artificial societies. Hence, it is not surprising to see that the time evolution of public health policies often show marked preferences for pre-selected segments of society. In this talk, I will discuss the role of my background and life experiences in shaping and driving my research program. Understanding the dynamics involved in identifying and shaping socially driven research programs can help others, particularly minority students, who often struggle to remain members of the mathematical sciences communities. The guilt that often accompanies those who want to help the have-nots, can be overcome in constructive and positive ways once we acknowledge that subjectivity does play a role and that basic research is an important foundation of our own socially-driven philosophies.

Roland Glowinski – "Looking at the Best Constant in a Sobolev Inequality: a Nonlinear Programming Approach"
       Abstract - Among the many things that Richard Tapia and this speaker have in common, they have a very deep admiration for Magnus Hestenes and his fundamental contributions to the Calculus of Variations, Control Theory and other areas of Optimization and Applied and Computational Mathematics. Recently the speaker became intrigued by the problem of finding the best constant in a Sobolev inequality involving the spaces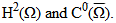
       This (kind of) non-smooth eigenvalue problem can be formulated as a constrained optimization problem from Calculus of Variations and can be solved by a methodology combining finite element approximations, an appropriate augmented Lagrangian, some convex duality and a touch of control. The speaker is confident that M. Hestenes would have loved both the problem and the solution method; one can hope that Richard Tapia, a former student of Hestenes at UCLA will like it to. If the ½ hour format allows it, an alternative approach based on the use of Green functions will be very briefly discussed.