Magma Dynamics
|
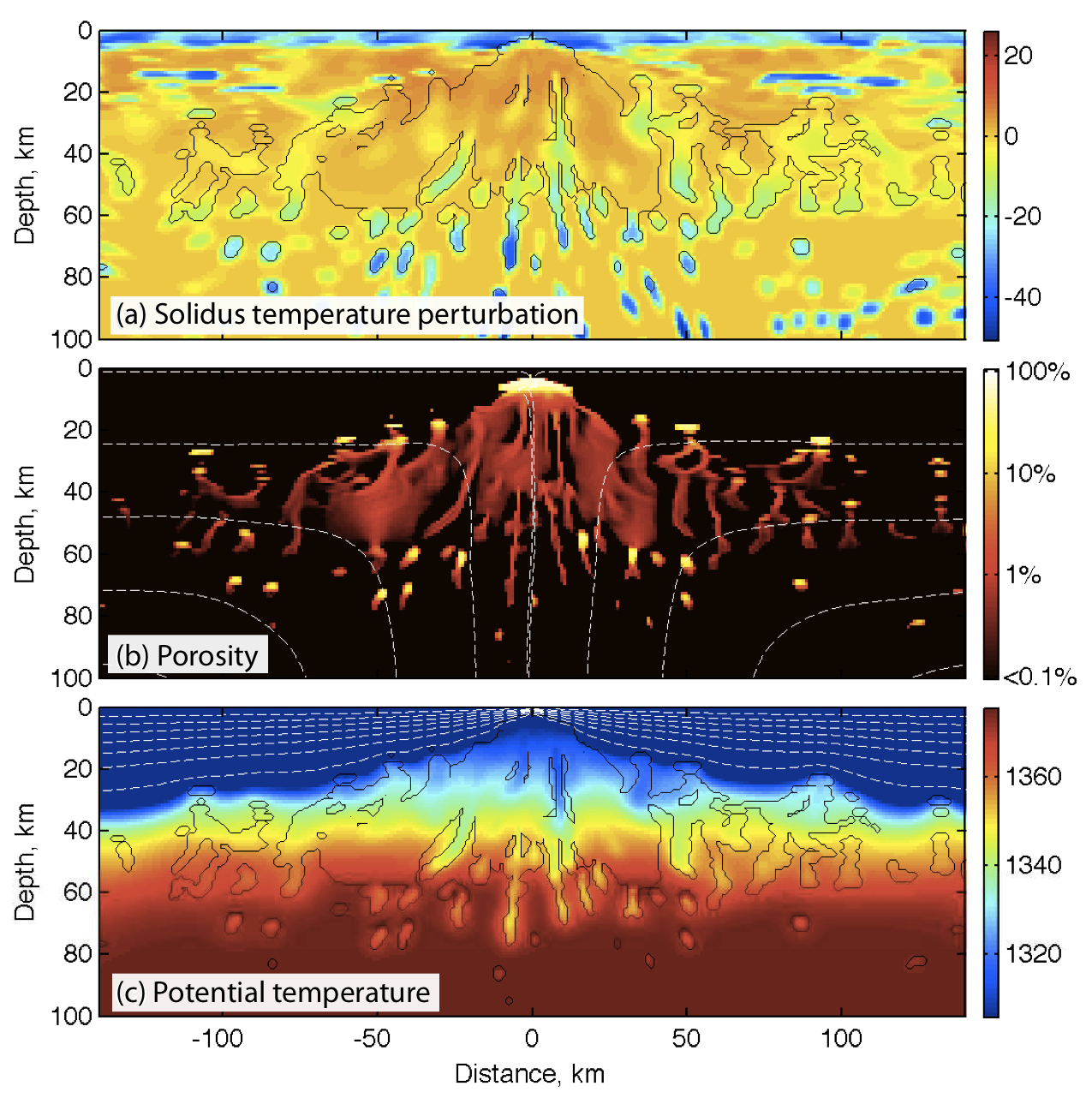
I am working with Richard Katz and Marc Spiegelman on magma dynamics problems, including the mid-ocean ridge spreading shown on the left. Magmatic plate boundaries (mid ocean ridges, subduction zones) and intra-plate hot spots are among the most important and complex dynamic and chemical systems in the solid earth. While volumetrically small, these regions have global consequences for mantle flow and plate tectonics through the spontaneous localization of weak plate boundaries. Magmatism in these regions also provides the dominant mechanism for geochemical fractionation, mixing and sampling of the Earth's mantle. Many of the observational constraints on both plate-boundary processes and global mantle dynamics come from regional studies of lavas from mid-ocean ridges, subduction zones and oceanic hot spots and form focus areas for many initiatives such as GeoPRISMS, EarthScope and core EAR and MGG Geophysics programs. Optimal preconditioners for many multiphysics problems, such as variable-viscosity Stokes and thermal convection, arise by combining existing optimal preconditioners for individual blocks of the Jacobian, associated with a given physics. For instance, a classic Stokes preconditioner applies multigrid to the momentum balance and scaling to the mass balance, combining them multiplicatively, using one block elimination step. The PETSc composable solvers allow a user to define different preconditioners for each equation block, and also different combination methods, inclduing Schur complements, between sets of equations, and it can all be specified dynamically on the command line without any code changes. Thus, the same code that runs full LU to verify a solution can also scale optimally on the largest machines available. Moreover, we can choose to split at various levels. Multigrid could be used for the overall Stokes system, and then splitting can be used for each smoother (so-called segregated KKT smoothers), inverting the classical scheme above. Finally, we can use split schemes to precondition the fully-coupled problem. In addition, we have recently introduced nonlinear preconditioning for the magma system, following this paper. We use nonlinear FAS multigrid preconditioned by Nonlinear CG. The tests can be found here. |
Papers
- In this paper, we describe the implementation of a subduction simulation using PETSc, and describe the mapping of geodynamics problems to PETSc components. Geodynamics simulations are characterized by rheological nonlinearity, localization, three-dimensional effects, and separate but interacting length scales. These features represent a challenge for computational science. We discuss how a leading software framework for advanced scientific computing (the Portable Extensible Toolkit for Scientific Computation, PETSc) can facilitate the development of geodynamics simulations. To illustrate our use of PETSc, we describe simulations of (i) steady-state, non-Newtonian passive flow and thermal structure beneath a mid-ocean ridge, (ii) magmatic solitary waves in the mantle, and (iii) the formation of localized bands of high porosity in a two-phase medium being deformed under simple shear. We highlight two supplementary features of PETSc, structured storage of application parameters and self-documenting output, that are especially useful for geodynamics simulations.